Ako nájsť vlastné hodnoty matice. Maticová charakteristická rovnica

www.stránka vám umožní nájsť. Stránka vykoná výpočet. Za niekoľko sekúnd server poskytne správne riešenie. Charakteristická rovnica pre maticu bude algebraický výraz nájdený pravidlom na výpočet determinantu matice matice, pričom na hlavnej uhlopriečke budú rozdiely v hodnotách prvkov uhlopriečky a premennej. Pri výpočte charakteristická rovnica pre maticu online, každý prvok matice budú vynásobené zodpovedajúcimi ďalšími prvkami matice. Nájsť v režime online možné len pre štvorec matice. Nájsť operáciu charakteristická rovnica pre maticu online redukuje na výpočet algebraického súčtu súčinu prvkov matice v dôsledku nájdenia determinantu matice, len za účelom určenia charakteristická rovnica pre maticu online. Táto operácia zaujíma v teórii osobitné miesto matice, vám umožňuje nájsť vlastné hodnoty a vektory pomocou koreňov. Hľadanie úlohy charakteristická rovnica pre maticu online je množiť prvky matice s následným sčítaním týchto produktov podľa určitého pravidla. www.stránka nájde charakteristická rovnica pre maticu daný rozmer v režime online. kalkulácia charakteristická rovnica pre maticu online pre danú dimenziu je to nájdenie polynómu s číselnými alebo symbolickými koeficientmi nájdenými pravidlom na výpočet determinantu matice- ako súčet súčinov zodpovedajúcich prvkov matice, len za účelom určenia charakteristická rovnica pre maticu online. Nájdenie polynómu vzhľadom na premennú pre štvorec matice, ako definícia charakteristická rovnica pre maticu, teoreticky bežné matice. Hodnota koreňov polynómu charakteristická rovnica pre maticu online používa sa na definovanie vlastných vektorov a vlastných hodnôt pre matice. Ak však determinant matice bude teda nula maticová charakteristická rovnica bude stále existovať, na rozdiel od naopak matice. Aby bolo možné vypočítať charakteristická rovnica pre maticu alebo vyhľadajte niekoľko naraz matice charakteristické rovnice, musíte stráviť veľa času a úsilia, kým náš server nájde charakteristická rovnica pre online maticu. V tomto prípade odpoveď nájdením charakteristická rovnica pre maticu online budú správne a s dostatočnou presnosťou, aj keď čísla pri náleze charakteristická rovnica pre maticu online bude iracionálne. Na strane www.stránka v prvkoch sú povolené znaky matice, teda charakteristická rovnica pre online maticu môžu byť pri výpočte reprezentované vo všeobecnej symbolickej forme matica charakteristických rovníc online. Získanú odpoveď je užitočné skontrolovať pri riešení problému nájdenia charakteristická rovnica pre maticu online pomocou stránky www.stránka. Pri vykonávaní operácie výpočtu polynómu - charakteristická rovnica matice, je potrebné byť pri riešení tohto problému pozorný a mimoriadne koncentrovaný. Naša stránka vám zase pomôže skontrolovať vaše rozhodnutie o danej téme matica charakteristických rovníc online. Ak nemáte čas na dlhé kontroly vyriešených problémov, tak www.stránka bude určite pohodlnou pomôckou na kontrolu pri hľadaní a výpočte charakteristická rovnica pre maticu online.

S maticou A, ak existuje číslo l také, že AX = lX.

V tomto prípade sa volá číslo l vlastná hodnota operátor (matica A) zodpovedajúci vektoru X.

Inými slovami, vlastný vektor je vektor, ktorý sa pôsobením lineárneho operátora transformuje na kolineárny vektor, t.j. stačí vynásobiť nejakým číslom. Naproti tomu nevhodné vektory sa transformujú ťažšie.

Definíciu vlastného vektora napíšeme ako sústavu rovníc:

Presuňme všetky výrazy na ľavú stranu:

Posledný systém možno zapísať v maticovej forme takto:

(A - lE)X \u003d O

Výsledná sústava má vždy nulové riešenie X = O. Voláme také sústavy, v ktorých sa všetky voľné členy rovnajú nule homogénne. Ak je matica takéhoto systému štvorcová a jej determinant sa nerovná nule, potom podľa Cramerových vzorcov vždy dostaneme jedinečné riešenie - nulu. Dá sa dokázať, že systém má nenulové riešenia práve vtedy, ak je determinant tejto matice rovný nule, t.j.

|A – lE| = = 0

Táto rovnica s neznámym l sa nazýva charakteristická rovnica (charakteristický polynóm) matica A (lineárny operátor).

Dá sa dokázať, že charakteristický polynóm lineárneho operátora nezávisí od výberu bázy.

Napríklad nájdime vlastné hodnoty a vlastné vektory lineárneho operátora dané maticou A = .

Na tento účel zostavíme charakteristickú rovnicu |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2 l + l 2 - 36 \u003d l 2 - 2 l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; vlastné hodnoty l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Aby sme našli vlastné vektory, riešime dve sústavy rovníc

(A + 5E) X = O

(A - 7E) X = O

Pre prvý z nich bude mať tvar rozšírená matica

,

odkiaľ x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, t.j. X (1) \u003d (- (2/3) s; s).

Pre druhú z nich bude mať tvar rozšírená matica

,

odkiaľ x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, t.j. X (2) \u003d ((2/3) s 1; s 1).

Vlastnými vektormi tohto lineárneho operátora sú teda všetky vektory tvaru (-(2/3)c; c) s vlastnou hodnotou (-5) a všetky vektory tvaru ((2/3)c 1 ; c 1) s vlastnou hodnotou 7.

Dá sa dokázať, že matica operátora A v báze pozostávajúcej z jeho vlastných vektorov je diagonálna a má tvar:

,

kde l i sú vlastné hodnoty tejto matice.

Platí to aj naopak: ak je matica A v nejakej báze diagonálna, potom všetky vektory tejto bázy budú vlastnými vektormi tejto matice.

Dá sa tiež dokázať, že ak má lineárny operátor n párovo odlišných vlastných hodnôt, potom zodpovedajúce vlastné vektory sú lineárne nezávislé a matica tohto operátora v zodpovedajúcej báze má diagonálny tvar.

Vysvetlime si to na predchádzajúcom príklade. Vezmime si ľubovoľné nenulové hodnoty c a c 1 , ale také, že vektory X (1) a X (2) sú lineárne nezávislé, t.j. by tvorili základ. Napríklad, nech c \u003d c 1 \u003d 3, potom X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Overme si lineárnu nezávislosť týchto vektorov:

12 ≠ 0. V tomto novom základe bude mať matica A tvar A * = .

Aby sme to overili, použijeme vzorec A * = C -1 AC. Najprv nájdime C -1.

C-1 = ;

Kvadratické formy

kvadratická forma f (x 1, x 2, x n) z n premenných sa nazýva súčet, ktorého každý člen je buď druhou mocninou jednej z premenných, alebo súčinom dvoch rôznych premenných, braných s určitým koeficientom: f (x 1, x 2, x n) = (a ij = a ji).

Matica A zložená z týchto koeficientov sa nazýva matice kvadratická forma. To je vždy symetrické matica (t. j. matica symetrická podľa hlavnej uhlopriečky, a ij = a ji).

V maticovom zápise má kvadratická forma tvar f(X) = X T AX, kde

Naozaj

Napríklad napíšme kvadratickú formu v maticovom tvare.

Na tento účel nájdeme maticu kvadratickej formy. Jeho diagonálne prvky sa rovnajú koeficientom na druhej mocnine premenných a zostávajúce prvky sa rovnajú polovici zodpovedajúcich koeficientov kvadratickej formy. Preto

Maticový stĺpec premenných X nech získame nedegenerovanou lineárnou transformáciou maticového stĺpca Y, t.j. X = CY, kde C je nedegenerovaná matica rádu n. Potom kvadratická forma f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (CT AC)Y.

Pri nedegenerovanej lineárnej transformácii C má teda matica kvadratickej formy tvar: A * = CT AC.

Nájdime napríklad kvadratickú formu f(y 1, y 2) získanú z kvadratickej formy f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 lineárnou transformáciou.

Kvadratická forma je tzv kanonický(Má kanonický pohľad) ak všetky jeho koeficienty a ij = 0 pre i ≠ j, t.j.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Jeho matica je diagonálna.

Veta(tu nie je uvedený dôkaz). Akákoľvek kvadratická forma môže byť redukovaná na kanonickú formu pomocou nedegenerovanej lineárnej transformácie.

Napríklad zredukujme na kanonickú formu kvadratickú formu
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Ak to chcete urobiť, najprv vyberte úplný štvorec pre premennú x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 x 3 - x.

Teraz vyberieme celý štvorec pre premennú x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 \u003d
\u003d 2 (x 1 + x 2) 2 – 5 (x 2 – (1/10) x 3) 2 + (1/20) x 3 2.

Potom nedegenerovaná lineárna transformácia y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 a y 3 \u003d x 3 redukuje túto kvadratickú formu na kanonickú formu f (y 1, y 2, y 3 3 / 2) + 2 ( 2 y 2 ) + 2 + 0 y 3 2.

Všimnite si, že kanonická forma kvadratickej formy je definovaná nejednoznačne (rovnaká kvadratická forma môže byť redukovaná na kanonickú formu rôznymi spôsobmi). Avšak kanonické formy získané rôznymi metódami majú množstvo spoločných vlastností. Najmä počet členov s kladnými (zápornými) koeficientmi kvadratickej formy nezávisí od toho, ako je forma redukovaná na túto formu (napríklad v uvažovanom príklade budú vždy dva záporné a jeden kladný koeficient). Táto vlastnosť sa nazýva zákon zotrvačnosti kvadratických foriem.

Overme si to zredukovaním tej istej kvadratickej formy na kanonickú formu iným spôsobom. Začnime transformáciu s premennou x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d -3 (
+ 2* x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) \u0012 -3r
+ 3y 2 2 + 2y 3 2, kde y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 a y 3 \u003d x 1. Tu je negatívny koeficient -3 pre y 1 a dva kladné koeficienty 3 a 2 pre y 2 a y 3 (a pomocou inej metódy sme dostali negatívny koeficient (-5) pre y 2 a dva kladné koeficienty: 2 pre y 1 a 1/20 pre y 3).

Treba si tiež uvedomiť, že hodnosť matice kvadratickej formy, tzv hodnosť kvadratickej formy, sa rovná počtu nenulových koeficientov kanonickej formy a pri lineárnych transformáciách sa nemení.

Kvadratická forma f(X) sa nazýva pozitívne (negatívne) istý, ak pre všetky hodnoty premenných, ktoré nie sú súčasne rovné nule, je kladné, t.j. f(X) > 0 (záporné, t.j.
f(X)< 0).

Napríklad kvadratická forma f 1 (X) \u003d x 1 2 + x 2 2 je pozitívne definitívna, pretože je súčet štvorcov a kvadratická forma f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 je záporne určitá, pretože predstavuje to môže byť reprezentované ako f 2 (X) \u003d - (x 1 - x 2) 2.

Vo väčšine praktických situácií je stanovenie znamienkovej určitosti kvadratickej formy o niečo ťažšie, preto sa na to používa jedna z nasledujúcich viet (formulujeme ich bez dôkazov).

Veta. Kvadratická forma je kladná (záporná) definitívna vtedy a len vtedy, ak sú všetky vlastné hodnoty jej matice kladné (záporné).

Veta(Sylvesterovo kritérium). Kvadratická forma je kladne definitívna vtedy a len vtedy, ak sú všetky hlavné minority matice tejto formy kladné.

Major (roh) moll K-tý rád matice A n-tého rádu sa nazýva determinant matice, zložený z prvých k riadkov a stĺpcov matice A ().

Všimnite si, že pri záporno-definičných kvadratických formách sa znamienka hlavných maloletých striedajú a vedľajší prvok prvého poriadku musí byť záporný.

Napríklad skúmame kvadratickú formu f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 na znamienkovú určitosť.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2 l - 3 l + l 2) - 4 \u003d l 2 - 5 l + 2 \u003d 0; D = 25 - 8 = 17;
. Preto je kvadratická forma pozitívne definitívna.

Metóda 2. Hlavná vedľajšia matica prvého rádu A D 1 = a 11 = 2 > 0. Hlavná vedľajšia matica druhého rádu D 2 = = 6 - 4 = 2 > 0. Preto podľa Sylvesterovho kritéria je kvadratická forma pozitívne definitívna.

Skúmame inú kvadratickú formu na určenie znamienka, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metóda 1. Zostrojme maticu kvadratickej formy А = . Charakteristická rovnica bude mať tvar = (-2 - l)*
*(-3 - 1) - 4 = (6 + 2 1 + 3 1 + 1 2) - 4 = 12 + 5 1 + 2 = 0; D = 25 - 8 = 17;
. Preto je kvadratická forma negatívne definitívna.

Metóda 2. Hlavná vedľajšia matica prvého rádu A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Podľa Sylvesterovho kritéria je teda kvadratická forma negatívne definitívna (znaky hlavných maloletých sa striedajú, začínajúc od mínusu).

A ako ďalší príklad skúmame kvadratickú formu f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 na určenie znamienka.

Metóda 1. Zostrojme maticu kvadratickej formy А = . Charakteristická rovnica bude mať tvar = (2 - l)*
*(-3 - 1) - 4 = ( - 6 - 2 1 + 3 1 + 1 2) - 4 = 12 + 1 - 10 = 0; D = 1 + 40 = 41;
.

Jedno z týchto čísel je záporné a druhé kladné. Znaky vlastných hodnôt sú rôzne. Preto kvadratická forma nemôže byť ani záporne, ani kladne definitívna, t.j. táto kvadratická forma nie je znamienkovo ​​definovaná (môže nadobúdať hodnoty akéhokoľvek znamienka).

Spôsob 2. Hlavná vedľajšia matica prvého rádu A D 1 = a 11 = 2 > 0. Hlavná vedľajšia matica druhého rádu D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Inštrukcia

Číslo k sa nazýva vlastná hodnota (číslo) matice A, ak existuje vektor x, ktorý Ax=kx. (1) V tomto prípade sa vektor x nazýva vlastný vektor matice A, zodpovedajúci číslu k. V priestore R ^ n (pozri obr. 1) má matica A tvar ako na obrázku.

Je potrebné nastaviť problém hľadania a vektorov matice A. Nech je vlastný vektor x daný súradnicami. V maticovej forme sa zapíše ako stĺpcová matica, ktorá by mala byť pre pohodlie reprezentovaná ako transponovaný riadok. X=(x1,x2,…,xn)^T. Na základe (1), Ax-kx=0 alebo Ax-kEx=0, kde E je matica identity (jednotky na hlavnej diagonále, všetky ostatné prvky sú nuly). Potom (A-kE)x=0. (2)

Výraz (2) lineárnych homogénnych algebraických rovníc má nenulové riešenie (vlastný vektor). Preto sa hlavný determinant systému (2) rovná nule, teda |А-kE|=0. (3) Posledná rovnosť vlastnej hodnoty k sa nazýva charakteristická rovnica matice A a v rozšírenom tvare má tvar (pozri obr. 2).

Dosadením koreňa k charakteristickej rovnice do sústavy (2) vzniká homogénna sústava lineárnych rovníc s degenerovanou maticou (jej determinantom je nula). Každé nenulové riešenie tejto sústavy je vlastným vektorom matice A zodpovedajúcej danej vlastnej hodnote k (teda koreňu charakteristickej rovnice).

Príklad. Nájdite vlastné hodnoty a vektory matice A (pozri obr. 3). Riešenie. Charakteristická rovnica je znázornená na obr. 3. Rozviňte determinant a nájdite vlastné hodnoty matice, ktorými sú daná rovnica (3-k)(-1-k)-5=0, (k-3)(k+1)-5=0, k^2-2k-8=0. Jej korene sú k1=4, k2=-2

a) Vlastné vektory zodpovedajúce k1=4 nájdeme riešením sústavy (A-4kE)x=0. V tomto prípade je potrebná iba jedna z jej rovníc, pretože je známe, že determinant systému je rovný nule. Ak dáme x=(x1, x2)^T, potom prvá rovnica systému (1-4)x1+x2=0, -3x1+x2=0. Ak predpokladáme, že x1=1 (len nie nula), potom x2=3. Keďže pre homogénny systém s degenerovanou maticou existuje ľubovoľne veľa nenulových riešení, potom celá množina vlastných vektorov zodpovedajúcich prvej vlastnej hodnote x =C1(1, 3), C1=konšt.

b) Nájdite vlastné vektory zodpovedajúce k2=-2. Pri riešení sústavy (A+2kE)x=0 je jej prvá rovnica (3+2)x1+x2=0, 5x1+x2=0 Ak dáme x1=1, tak x2=-5. Zodpovedajúce vlastné vektory x =C2(1, 3), C2=konšt. Celková množina všetkých vlastných vektorov danej matice: x = C1(1, 3) + C2(1, 3).

Zdroje:

• Piskunov N.S. Diferenciálny a integrálny počet. M., 1976, - 576 s.
• nájsť vlastné hodnoty a maticové vektory

Matice, ktoré sú tabuľkovou formou zaznamenávania údajov, sú široko používané pri práci so sústavami lineárnych rovníc. Okrem toho počet rovníc určuje počet riadkov matice a počet premenných určuje poradie jej stĺpcov. Výsledkom je, že riešenie lineárnych systémov sa redukuje na operácie s maticami, jednou z nich je hľadanie vlastných hodnôt matíc. Ich výpočet sa vykonáva pomocou charakteristickej rovnice. Vlastné hodnoty možno definovať pre štvorcovú maticu rádu m.

Inštrukcia

Zapíšte daný štvorec A. Na zistenie jeho vlastných hodnôt použite charakteristickú rovnicu vyplývajúcu z podmienky pre netriviálne riešenie lineárneho homogénneho systému, v tomto prípade reprezentovaného štvorcovou maticou. Ako vyplýva z Cramera, riešenie existuje len vtedy, ak je jeho determinant nula. Môžeme teda napísať rovnicu | A-λE | = 0, kde А je dané číslo, λ sú požadované čísla, E je matica identity, v ktorej sú všetky prvky na hlavnej uhlopriečke rovné jednej a ostatné sú rovné nule.

Vynásobte požadovanú premennú λ identitou matice E rovnakej dimenzie ako zadaná iniciála A. Výsledkom operácie bude matica, kde hodnoty λ sú umiestnené pozdĺž hlavnej uhlopriečky, zvyšné prvky zostávajú rovné nule.

Matice diagonálneho typu sú najjednoduchšie usporiadané. Vzniká otázka, či je možné nájsť základ, v ktorom by matica lineárneho operátora mala diagonálny tvar. Takýto základ existuje.
Nech je daný lineárny priestor R n a v ňom pôsobiaci lineárny operátor A; v tomto prípade operátor A berie do seba R n, teda A:R n → R n .

Definícia. Nenulový vektor x sa nazýva vlastný vektor operátora A, ak operátor A transformuje x na vektor s ním kolineárny, t.j. Číslo λ sa nazýva vlastná hodnota alebo vlastná hodnota operátora A zodpovedajúceho vlastnému vektoru x .
Zaznamenávame niektoré vlastnosti vlastných hodnôt a vlastných vektorov.
1. Ľubovoľná lineárna kombinácia vlastných vektorov operátora A zodpovedajúceho rovnakej vlastnej hodnote λ je vlastný vektor s rovnakou vlastnou hodnotou.
2. Vlastné vektory operátor A s párovo odlišnými vlastnými hodnotami λ 1 , λ 2 , …, λ m sú lineárne nezávislé.
3. Ak vlastné hodnoty λ 1 =λ 2 = λ m = λ, potom vlastná hodnota λ zodpovedá nie viac ako m lineárne nezávislým vlastným vektorom.

Ak teda existuje n lineárne nezávislých vlastných vektorov zodpovedajúce rôznym vlastným hodnotám λ 1 , λ 2 , …, λ n , potom sú lineárne nezávislé, preto ich možno považovať za základ priestoru R n . Nájdite tvar matice lineárneho operátora A na základe jeho vlastných vektorov, pre ktoré pôsobíme s operátorom A na vektoroch báz: Potom .
Matica lineárneho operátora A má teda na základe svojich vlastných vektorov diagonálny tvar a vlastné hodnoty operátora A sú na diagonále.
Existuje iný základ, v ktorom má matica diagonálny tvar? Odpoveď na túto otázku dáva nasledujúca veta.

Veta. Matica lineárneho operátora A v báze (i = 1..n) má diagonálny tvar práve vtedy, ak všetky vektory bázy sú vlastné vektory operátora A.

Pravidlo na nájdenie vlastných hodnôt a vlastných vektorov

Nechajte vektor , kde x 1 , x 2 , …, x n - súradnice vektora x vzhľadom na základ a x je vlastný vektor lineárneho operátora A zodpovedajúci vlastnej hodnote λ, t.j. Tento vzťah je možné zapísať v maticovom tvare

. (*)

Rovnicu (*) možno považovať za rovnicu na nájdenie x , a , to znamená, že nás zaujímajú netriviálne riešenia, pretože vlastný vektor nemôže byť nula. Je známe, že netriviálne riešenia homogénneho systému lineárnych rovníc existujú práve vtedy, ak det(A - λE) = 0. Aby teda λ bolo vlastnou hodnotou operátora A, je potrebné a postačujúce, aby det(A - λE) = 0.
Ak je rovnica (*) napísaná podrobne v súradnicovom tvare, dostaneme systém lineárnych homogénnych rovníc:

(1)
Kde je matica lineárneho operátora.

Sústava (1) má nenulové riešenie, ak sa jej determinant D rovná nule

Dostali sme rovnicu na nájdenie vlastných hodnôt.
Táto rovnica sa nazýva charakteristická rovnica a jej ľavá strana sa nazýva charakteristický polynóm matice (operátor) A. Ak charakteristický polynóm nemá reálne korene, potom matica A nemá žiadne vlastné vektory a nemôže byť redukovaná do diagonálneho tvaru.
Nech λ 1 , λ 2 , …, λ n sú skutočné korene charakteristickej rovnice a môžu byť medzi nimi násobky. Nahradením týchto hodnôt do systému (1) nájdeme vlastné vektory.

Príklad 12. Lineárny operátor A pôsobí v R 3 podľa zákona , kde x 1 , x 2 , .., x n sú súradnice vektora v zákl. , , . Nájdite vlastné hodnoty a vlastné vektory tohto operátora.
Riešenie. Vytvoríme maticu tohto operátora:
.
Zostavíme systém na určenie súradníc vlastných vektorov:

Zostavíme charakteristickú rovnicu a vyriešime ju:

.
λ 1,2 = -1, λ 3 = 3.
Dosadením λ = -1 do systému máme:
alebo
Pretože , potom existujú dve závislé premenné a jedna voľná premenná.
Nech je x 1 voľná neznáma Túto sústavu vyriešime ľubovoľným spôsobom a nájdeme všeobecné riešenie tejto sústavy: Základná sústava riešení pozostáva z jedného riešenia, keďže n - r = 3 - 2 = 1.
Množina vlastných vektorov zodpovedajúcich vlastnej hodnote λ = -1 má tvar: , kde x 1 je ľubovoľné číslo iné ako nula. Vyberme si jeden vektor z tejto množiny, napríklad nastavením x 1 = 1: .
Ak budeme argumentovať podobne, nájdeme vlastný vektor zodpovedajúci vlastnej hodnote λ = 3: .
V priestore R 3 bázu tvoria tri lineárne nezávislé vektory, ale získali sme len dva lineárne nezávislé vlastné vektory, z ktorých bázu v R 3 nemožno vytvoriť. V dôsledku toho maticu A lineárneho operátora nemožno redukovať na diagonálny tvar.

Príklad 13 Daná matica .
1. Dokážte, že vektor je vlastný vektor matice A. Nájdite vlastnú hodnotu zodpovedajúcu tomuto vlastnému vektoru.
2. Nájdite základ, v ktorom má matica A diagonálny tvar.
Riešenie.
1. Ak , potom x je vlastný vektor

.
Vektor (1, 8, -1) je vlastný vektor. Vlastná hodnota λ = -1.
Matica má diagonálny tvar v základe pozostávajúcom z vlastných vektorov. Jeden z nich je známy. Poďme nájsť zvyšok.
Hľadáme vlastné vektory zo systému:

Charakteristická rovnica: ;
(3+A)[-2(2-A)(2+A)+3] = 0; (3+A)(A2-1) = 0
λ1 = -3, λ2 = 1, λ3 = -1.
Nájdite vlastný vektor zodpovedajúci vlastnej hodnote λ = -3:

Hodnosť matice tohto systému sa rovná dvom a rovná sa počtu neznámych, preto má tento systém iba nulové riešenie x 1 = x 3 = 0. x 2 tu môže byť čokoľvek iné ako nula, napríklad x 2 = 1. Vektor (0,1,0) je teda vlastný vektor zodpovedajúci λ = -3. Skontrolujme to:
.
Ak λ = 1, dostaneme systém
Hodnosť matice je dva. Prečiarknite poslednú rovnicu.
Nech x 3 je voľná neznáma. Potom x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Za predpokladu, že x 3 = 1, máme (-3,-9,1) - vlastný vektor zodpovedajúci vlastnej hodnote λ = 1. Skontrolujte:

.
Pretože vlastné hodnoty sú skutočné a rôzne, vektory, ktoré im zodpovedajú, sú lineárne nezávislé, takže ich možno brať ako základ v R3. Teda v zákl , , matica A má tvar:
.
Nie každú maticu lineárneho operátora A:R n → R n možno redukovať na diagonálny tvar, pretože pre niektoré lineárne operátory môže existovať menej ako n lineárne nezávislých vlastných vektorov. Ak je však matica symetrická, potom presne m lineárne nezávislých vektorov zodpovedá koreňu charakteristickej rovnice násobnosti m.

Definícia. Symetrická matica je štvorcová matica, v ktorej sú prvky, ktoré sú symetrické vzhľadom na hlavnú uhlopriečku, rovnaké, to znamená, v ktorej .
Poznámky. 1. Všetky vlastné hodnoty symetrickej matice sú skutočné.
2. Vlastné vektory symetrickej matice zodpovedajúce párovo odlišným vlastným hodnotám sú ortogonálne.
Za jednu z početných aplikácií študovaného aparátu považujeme problém určenia tvaru krivky druhého rádu.

". Prvá časť načrtáva ustanovenia, ktoré sú minimálne potrebné na pochopenie chemometrie, a druhá časť obsahuje fakty, ktoré potrebujete vedieť pre hlbšie pochopenie metód viacrozmernej analýzy. Prezentácia je ilustrovaná príkladmi vytvorenými v excelovom zošite Matrix.xls ktorý je priložený k tomuto dokumentu.

Odkazy na príklady sú v texte umiestnené ako objekty programu Excel. Tieto príklady sú abstraktného charakteru, nie sú nijako viazané na problémy analytickej chémie. Reálne príklady využitia maticovej algebry v chemometrii sú rozoberané v iných textoch venovaných rôznym chemometrickým aplikáciám.

Väčšina meraní uskutočňovaných v analytickej chémii nie sú priame, ale nepriamy. To znamená, že v experimente sa namiesto hodnoty požadovaného analytu C (koncentrácia) získa iná hodnota X(signál) súvisiaci, ale nie rovný C, t.j. X(C) ≠ C. Spravidla typ závislosti X(C) nie je známe, ale našťastie v analytickej chémii je väčšina meraní proporcionálna. To znamená, že ako koncentrácia C in a krát sa signál X zvýši o rovnakú hodnotu, t.j. X(a C) = a x(C). Okrem toho sú signály aj aditívne, takže signál zo vzorky obsahujúcej dve látky s koncentráciami C 1 a C 2 sa bude rovnať súčtu signálov z každej zložky, t.j. X(C1 + C2) = X(C1)+ X(C2). Proporcionalita a aditívnosť spolu dávajú linearita. Na ilustráciu princípu linearity možno uviesť mnoho príkladov, ale stačí spomenúť dva najvýraznejšie príklady – chromatografiu a spektroskopiu. Druhým znakom experimentu v analytickej chémii je viackanálový. Moderné analytické zariadenia súčasne merajú signály pre mnoho kanálov. Napríklad intenzita priepustnosti svetla sa meria pre viacero vlnových dĺžok naraz, t.j. rozsah. Preto sa v experimente zaoberáme rôznymi signálmi X 1 , X 2 ,...., X n charakterizujúce súbor koncentrácií C 1 ,C 2, ..., C m látok prítomných v skúmanom systéme.

Ryža. 1 Spectra

Analytický experiment je teda charakterizovaný linearitou a multidimenzionálnosťou. Preto je vhodné považovať experimentálne dáta za vektory a matice a manipulovať s nimi pomocou aparátu maticovej algebry. Úspešnosť tohto prístupu ilustruje príklad uvedený v , ktorý ukazuje tri spektrá pre 200 vlnových dĺžok od 4000 do 4796 cm–1. Najprv ( X 1) a druhý ( X 2) spektrá boli získané pre štandardné vzorky, v ktorých sú známe koncentrácie dvoch látok A a B: v prvej vzorke [A] = 0,5, [B] = 0,1 a v druhej vzorke [A] = 0,2, [B] = 0,6. Čo možno povedať o novej, neznámej vzorke, ktorej spektrum je uvedené X 3 ?

Zvážte tri experimentálne spektrá X 1 , X 2 a X 3 ako tri vektory dimenzie 200. Pomocou lineárnej algebry sa to dá ľahko ukázať X 3 = 0.1 X 1 +0.3 X 2, takže tretia vzorka zjavne obsahuje len látky A a B v koncentráciách [A] = 0,5×0,1 + 0,2×0,3 = 0,11 a [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Základné informácie

1.1 Matrice

Matrix nazývaná napríklad obdĺžniková tabuľka čísel

Ryža. 2 Matica

Matice sú označené veľkými tučnými písmenami ( A), a ich prvky - so zodpovedajúcimi malými písmenami s indexmi, t.j. a ij . Prvý index čísluje riadky a druhý číslo stĺpce. V chemometrii je zvykom označovať maximálnu hodnotu indexu rovnakým písmenom ako samotný index, ale veľkými písmenami. Preto matica A možno napísať aj ako ( a ij , i = 1,..., ja; j = 1,..., J). Pre príklad matice ja = 4, J= 3 a a 23 = −7.5.

Dvojica čísel ja A J sa nazýva rozmer matice a označuje sa ako ja× J. Príkladom matrice v chemometrii je súbor spektier získaných pre ja vzorky na J vlnové dĺžky.

1.2. Najjednoduchšie operácie s maticami

Matice môžu vynásobte číslami. V tomto prípade sa každý prvok vynásobí týmto číslom. Napríklad -

Ryža. 3 Násobenie matice číslom

Dve matice rovnakej dimenzie môžu byť elementárne zložiť A odčítať. Napríklad,

Ryža. 4 Pridanie matice

Násobením číslom a sčítaním sa získa matica rovnakého rozmeru.

Nulová matica je matica pozostávajúca z núl. Je určený O. To je zrejmé A+O = A, A−A = O a 0 A = O.

Matica môže transponovať. Pri tejto operácii sa matrica preklopí, t.j. riadky a stĺpce sú vymenené. Transpozícia je označená pomlčkou, A“ alebo index A t . Teda ak A = {a ij , i = 1,..., ja; j = 1,...,J), To A t = ( a ji , j = 1,...,J; i = 1,..., ja). Napríklad

Ryža. 5 Maticová transpozícia

Je zrejmé, že ( A t) t = A, (A+B) t = A t+ B t .

1.3. Maticové násobenie

Matice môžu množiť, ale iba ak majú príslušné rozmery. Prečo je to tak, bude zrejmé z definície. Matrixový produkt A, rozmer ja× K a matrice B, rozmer K× J, sa nazýva matica C, rozmer ja× J, ktorého prvkami sú čísla

Teda pre produkt AB je potrebné, aby počet stĺpcov v ľavej matici A sa rovnalo počtu riadkov v pravej matici B. Príklad produktu Matrix -

Obr.6 Súčin matíc

Pravidlo násobenia matice môže byť formulované nasledovne. Na nájdenie prvku matice C stojaci na križovatke i-tý riadok a j-tý stĺpec ( c ij) sa musí vynásobiť prvok po prvku i-tý riadok prvej matice A na j-tý stĺpec druhej matice B a spočítajte všetky výsledky. Takže v zobrazenom príklade sa prvok z tretieho riadka a druhého stĺpca získa ako súčet prvkov po prvkoch v treťom riadku. A a druhý stĺpec B

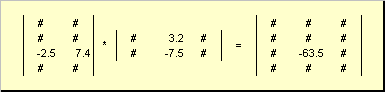
Obr.7 Prvok súčinu matíc

Súčin matríc závisí od poradia, t.j. AB ≠ BA, aspoň z rozmerových dôvodov. Hovorí sa, že je nekomutatívna. Súčin matíc je však asociatívny. Znamená to, že ABC = (AB)C = A(BC). Navyše je aj distributívny, t.j. A(B+C) = AB+AC. To je zrejmé AO = O.

1.4. Štvorcové matice

Ak sa počet stĺpcov matice rovná počtu jej riadkov ( ja = J=N), potom sa takáto matica nazýva štvorcová. V tejto časti sa budeme zaoberať iba takýmito maticami. Medzi týmito maticami je možné vyčleniť matice so špeciálnymi vlastnosťami.

Samotársky matica (označená ja a niekedy E) je matica, v ktorej sa všetky prvky rovnajú nule, okrem diagonálnych, ktoré sa rovnajú 1, t.j.

Samozrejme AI = IA = A.

Matica sa nazýva uhlopriečka, ak všetky jeho prvky okrem diagonálnych ( a ii) sa rovnajú nule. Napríklad

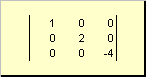
Ryža. 8 Diagonálna matica

Matrix A nazývaný vrchol trojuholníkový, ak sa všetky jeho prvky ležiace pod uhlopriečkou rovnajú nule, t.j. a ij= 0, pri i>j. Napríklad

Ryža. 9 Horná trojuholníková matrica

Spodná trojuholníková matica je definovaná podobne.

Matrix A volal symetrické, Ak A t = A. Inými slovami a ij = a ji. Napríklad

Ryža. 10 Symetrická matica

Matrix A volal ortogonálne, Ak

A t A = AA t = ja.

Matica sa nazýva normálne Ak

1.5. Stopa a determinant

Sledovanieštvorcovú maticu A(označené Tr( A) alebo Sp( A)) je súčet jeho diagonálnych prvkov,

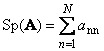
Napríklad,

Ryža. 11 Maticová stopa

To je zrejmé

Sp(a A) = α Sp( A) A

Sp( A+B) = Sp( A)+ Sp( B).

Dá sa to ukázať

Sp( A) = Sp( A t), Sp( ja) = N,

a tiež to

Sp( AB) = Sp( BA).

Ďalšou dôležitou vlastnosťou štvorcovej matice je jej determinant(označené det( A)). Definícia determinantu vo všeobecnom prípade je pomerne komplikovaná, takže začneme najjednoduchšou možnosťou - maticou A rozmer (2×2). Potom

Pre maticu (3×3) sa determinant bude rovnať

V prípade matice ( N× N) determinant sa vypočíta ako súčet 1 2 3 ... N= N! termíny, z ktorých každý sa rovná

indexy k 1 , k 2 ,..., k N sú definované ako všetky možné usporiadané permutácie rčísla v sade (1, 2, ... , N). Výpočet maticového determinantu je zložitý postup, ktorý sa v praxi vykonáva pomocou špeciálnych programov. Napríklad,

Ryža. 12 Maticový determinant

Zaznamenávame iba zrejmé vlastnosti:

det( ja) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. vektory

Ak má matica iba jeden stĺpec ( J= 1), potom sa takýto objekt nazýva vektor. Presnejšie, stĺpcový vektor. Napríklad

Za matice pozostávajúce z jedného radu možno považovať aj napr

Tento objekt je tiež vektor, ale riadkový vektor. Pri analýze údajov je dôležité pochopiť, s ktorými vektormi sa zaoberáme - stĺpcami alebo riadkami. Takže spektrum odobraté pre jednu vzorku možno považovať za riadkový vektor. Potom by sa súbor spektrálnych intenzít pri určitej vlnovej dĺžke pre všetky vzorky mal považovať za stĺpcový vektor.

Rozmer vektora je počet jeho prvkov.

Je jasné, že akýkoľvek stĺpcový vektor možno transpozíciou transformovať na riadkový, t.j.

V tých prípadoch, kde nie je špecificky špecifikovaná forma vektora, ale hovorí sa jednoducho o vektore, znamenajú stĺpcový vektor. Toto pravidlo dodržíme aj my. Vektor je označený malým priamym tučným písmenom. Nulový vektor je vektor, ktorého všetky prvky sú rovné nule. Označuje sa 0 .

1.7. Najjednoduchšie operácie s vektormi

Vektory možno sčítať a násobiť číslami rovnakým spôsobom ako matice. Napríklad,

Ryža. 13 Operácie s vektormi

Dva vektory X A r volal kolineárne, ak existuje číslo α také, že

1.8. Produkty vektorov

Dva vektory rovnakej dimenzie N možno znásobiť. Nech sú dva vektory X = (X 1 , X 2 ,...,X N) t a r = (r 1 , r 2 ,...,r N) t. Podľa pravidla násobenia „riadok po stĺpci“ z nich môžeme vyrobiť dva produkty: X t r A xy t . Prvá práca

volal skalárne alebo interné. Jeho výsledkom je číslo. Používa tiež notáciu ( X,r)= X t r. Napríklad,

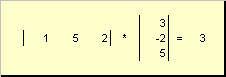
Ryža. 14 Vnútorný (skalárny) súčin

Druhá práca

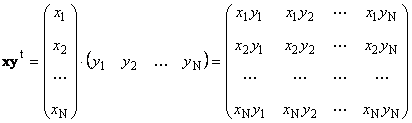
volal externé. Jeho výsledkom je matica rozmerov ( N× N). Napríklad,

Ryža. 15 Vonkajší produkt

Volajú sa vektory, ktorých skalárny súčin sa rovná nule ortogonálne.

1.9. Vektorová norma

Skalárny súčin vektora so sebou samým sa nazýva skalárny štvorec. Táto hodnota

definuje štvorec dĺžka vektor X. Na označenie dĺžky (tzv normou vektor) používa sa zápis

Napríklad,

Ryža. 16 Vektorová norma

Vektor jednotkovej dĺžky (|| X|| = 1) sa nazýva normalizovaný. Nenulový vektor ( X ≠ 0 ) možno normalizovať vydelením dĺžkou, t.j. X = ||X|| (X/||X||) = ||X|| e. Tu e = X/||X|| je normalizovaný vektor.

Vektory sa nazývajú ortonormálne, ak sú všetky normalizované a párovo ortogonálne.

1.10. Uhol medzi vektormi

Skalárny súčin definuje a rohuφ medzi dvoma vektormi X A r

Ak sú vektory ortogonálne, potom cosφ = 0 a φ = π/2, a ak sú kolineárne, potom cosφ = 1 a φ = 0.

1.11. Vektorové znázornenie matice

Každá matrica A veľkosť ja× J môžu byť reprezentované ako množina vektorov

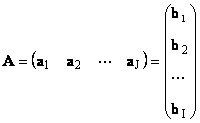
Tu je každý vektor a j je j-tý stĺpcový a riadkový vektor b i je i-tý riadok matice A

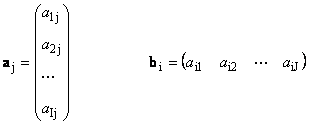
1.12. Lineárne závislé vektory

vektory rovnakej dimenzie ( N) možno sčítať a vynásobiť číslom, rovnako ako matice. Výsledkom je vektor rovnakej dimenzie. Nech existuje niekoľko vektorov rovnakej dimenzie X 1 , X 2 ,...,X K a rovnaký počet čísel α α 1 , α 2 ,...,α K. Vektor

r= α 1 X 1 + α 2 X 2 +...+α K X K

volal lineárna kombinácia vektory X k .

Ak existujú také nenulové čísla α k ≠ 0, k = 1,..., K, Čo r = 0 , potom takáto množina vektorov X k volal lineárne závislé. V opačnom prípade sa vektory nazývajú lineárne nezávislé. Napríklad vektory X 1 = (2, 2) ta X 2 = (−1, −1) t sú lineárne závislé, keďže X 1 +2X 2 = 0

1.13. Hodnosť matice

Zvážte súbor K vektory X 1 , X 2 ,...,X K rozmery N. Hodnosť tohto systému vektorov je maximálny počet lineárne nezávislých vektorov. Napríklad v súprave

existujú napríklad len dva lineárne nezávislé vektory X 1 a X 2, takže jeho poradie je 2.

Je zrejmé, že ak je v množine viac vektorov, ako je ich rozmer ( K>N), potom sú nevyhnutne lineárne závislé.

Hodnosť matice(označené hodnosťou ( A)) je poradie systému vektorov, z ktorých pozostáva. Hoci akákoľvek matica môže byť reprezentovaná dvoma spôsobmi (stĺpcovými vektormi alebo riadkovými vektormi), nemá to vplyv na hodnotu poradia, pretože

1.14. inverzná matica

štvorcovú maticu A sa nazýva nedegenerovaný, ak má jedinečný obrátene matice A-1 , určené podmienkami

AA −1 = A −1 A = ja.

Inverzná matica neexistuje pre všetky matice. Nevyhnutnou a postačujúcou podmienkou pre nedegeneráciu je

det( A) ≠ 0 alebo poradie ( A) = N.

Inverzia matice je zložitý postup, na ktorý existujú špeciálne programy. Napríklad,

Ryža. 17 Inverzia matice

Uvádzame vzorce pre najjednoduchší prípad - matice 2 × 2

Ak matriky A A B sú teda nedegenerované

(AB) −1 = B −1 A −1 .

1.15. Pseudoinverzná matica

Ak matica A je degenerovaný a inverzná matica neexistuje, potom v niektorých prípadoch možno použiť pseudoinverzný matice, ktorá je ako taká matica definovaná A+ to

AA + A = A.

Pseudoinverzná matica nie je jediná a jej forma závisí od spôsobu konštrukcie. Napríklad pre obdĺžnikovú maticu môžete použiť metódu Moore-Penrose.

Ak je počet stĺpcov menší ako počet riadkov, potom

A + =(A t A) −1 A t

Napríklad,

Ryža. 17a Pseudomaticová inverzia

Ak je počet stĺpcov väčší ako počet riadkov, potom

A + =A t( AA t) −1

1.16. Násobenie vektora maticou

Vektor X možno vynásobiť maticou A vhodný rozmer. V tomto prípade sa stĺpcový vektor vynásobí vpravo Ax a vektorový reťazec je vľavo X t A. Ak je rozmer vektora J a rozmer matice ja× J výsledkom je potom vektor dimenzie ja. Napríklad,

Ryža. 18 Vektorovo-maticové násobenie

Ak matica A- námestie ( ja× ja), potom vektor r = Ax má rovnaký rozmer ako X. To je zrejmé

A(α 1 X 1 + α 2 X 2) = a 1 Ax 1 + α 2 Ax 2 .

Matice preto možno považovať za lineárne transformácie vektorov. Najmä X = X, Vôl = 0 .

2. Ďalšie informácie

2.1. Sústavy lineárnych rovníc

Nechaj A- veľkosť matrice ja× J, A b- rozmerový vektor J. Zvážte rovnicu

Ax = b

vzhľadom na vektor X, rozmery ja. V podstate ide o systém ja lineárne rovnice s J neznámy X 1 ,...,X J. Riešenie existuje vtedy a len vtedy

hodnosť ( A) = poradie ( B) = R,

Kde B je rozšírená matica dimenzií ja×( J+1) pozostávajúce z matrice A, čalúnený stĺpom b, B = (A b). V opačnom prípade sú rovnice nekonzistentné.

Ak R = ja = J, potom je riešenie jedinečné

X = A −1 b.

Ak R < ja, potom existuje veľa rôznych riešení, ktoré možno vyjadriť pomocou lineárnej kombinácie J−R vektory. Systém homogénnych rovníc Ax = 0 so štvorcovou maticou A (N× N) má netriviálne riešenie ( X ≠ 0 ) vtedy a len vtedy, ak det( A) = 0. Ak R= poradie( A)<N, potom existujú N−R lineárne nezávislé riešenia.

2.2. Bilineárne a kvadratické formy

Ak A je štvorcová matica a X A r- vektory zodpovedajúcej dimenzie, potom skalárny súčin tvaru X t Áno volal bilineárne tvar definovaný maticou A. O X = r výraz X t Ax volal kvadratický formulár.

2.3. Pozitívne definitívne matice

štvorcovú maticu A volal kladné definitívne, ak pre akýkoľvek nenulový vektor X ≠ 0 ,

X t Ax > 0.

The negatívne (X t Ax < 0), nezáporné (X t Ax≥ 0) a nepozitívne (X t Ax≤ 0) určité matice.

2.4. Choleský rozklad

Ak je symetrická matica A je pozitívne definitívna, potom existuje jedinečná trojuholníková matica U s pozitívnymi prvkami, pre ktoré

A = U t U.

Napríklad,

Ryža. 19 Choleský rozklad

2.5. polárny rozklad

Nechaj A je nesingulárna štvorcová matica rozmerov N× N. Potom je tu unikát polárny výkon

A = SR,

Kde S je nezáporná symetrická matica a R je ortogonálna matica. matice S A R možno definovať explicitne:

S 2 = AA t alebo S = (AA t) ½ a R = S −1 A = (AA t) -½ A.

Napríklad,

Ryža. 20 Polárny rozklad

Ak matica A je degenerovaný, potom rozklad nie je jedinečný - konkrétne: S stále sám, ale R môže byť veľa. Polárny rozklad predstavuje maticu A ako kombinácia kompresie/natiahnutia S a sústruženie R.

2.6. Vlastné vektory a vlastné hodnoty

Nechaj A je štvorcová matica. Vektor v volal vlastný vektor matice A, Ak

Av = λ v,

kde sa volá číslo λ vlastná hodnota matice A. Teda transformácia, ktorú matica vykonáva A nad vektorom v, sa redukuje na jednoduché natiahnutie alebo stlačenie s faktorom λ. Vlastný vektor je určený až po násobenie konštantou α ≠ 0, t.j. Ak v je vlastný vektor, potom α v je tiež vlastný vektor.

2.7. Vlastné hodnoty

Na matrice A, rozmer ( N× N) nemôže byť väčšia ako N vlastné hodnoty. Uspokojujú charakteristická rovnica

det( A − λ ja) = 0,

čo je algebraická rovnica N- poradie. Najmä pre maticu 2×2 má charakteristická rovnica tvar

Napríklad,

Ryža. 21 Vlastné hodnoty

Množina vlastných hodnôt λ 1 ,..., λ N matice A volal spektrum A.

Spektrum má rôzne vlastnosti. Najmä

det( A) = λ 1×...×λ N, Sp( A) = λi +...+λ N.

Vlastné hodnoty ľubovoľnej matice môžu byť komplexné čísla, ale ak je matica symetrická ( A t = A), potom sú jeho vlastné hodnoty skutočné.

2.8. Vlastné vektory

Na matrice A, rozmer ( N× N) nemôže byť väčšia ako N vlastné vektory, z ktorých každý zodpovedá svojej vlastnej hodnote. Na určenie vlastného vektora v n musíte vyriešiť systém homogénnych rovníc

(A − λ n ja)v n = 0 .

Má to netriviálne riešenie, pretože det( A-λ n ja) = 0.

Napríklad,

Ryža. 22 Vlastné vektory

Vlastné vektory symetrickej matice sú ortogonálne.

Facebook

Twitter

V kontakte s

Spolužiaci

Google+