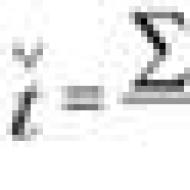A másodfokú forma mátrixjelölésének van formája. Pozitív határozott másodfokú formák
Pozitív határozott másodfokú formák
Meghatározás. Másodfokú forma -tól n ismeretlennek hívják pozitív határozott, ha rangja egyenlő a pozitív tehetetlenségi indexszel és egyenlő az ismeretlenek számával.
Tétel. A másodfokú forma akkor és csak akkor pozitív határozott, ha bármely nem nulla változóérték-készleten vesz fel pozitív értékeket.
Bizonyíték. Legyen a másodfokú alak az ismeretlenek nem degenerált lineáris transzformációja
normalizálódott
.
Bármely nem nulla változóérték-készlet esetén legalább egy számot 
nullától eltérő, azaz. . A tétel szükségessége bizonyítást nyert.
Tegyük fel, hogy a másodfokú forma bármely nem nulla változóhalmazra pozitív értéket vesz fel, de tehetetlenségi indexe pozitív. Az ismeretlenek nem degenerált lineáris transzformációjával
Állítsuk vissza a normális kerékvágásba. Az általánosság elvesztése nélkül feltételezhetjük, hogy ebben a normálalakban az utolsó változó négyzete vagy hiányzik, vagy mínusz előjellel lép be, pl. 
, hol vagy . Tegyük fel, hogy ez a változók nullától eltérő értékkészlete, amelyet a lineáris egyenletrendszer megoldása eredményeként kapunk
Ebben a rendszerben az egyenletek száma megegyezik a változók számával, és a rendszer determinánsa nem nulla. Cramer tétele szerint a rendszernek egyedi megoldása van, és ez nem nulla. Ehhez a készlethez. Ellentmondás a feltétellel. A feltételezéssel ellentmondáshoz jutunk, ami a tétel elégségességét bizonyítja.
Ezzel a kritériummal az együtthatókból nem lehet meghatározni, hogy egy másodfokú alak pozitív-definit-e. Erre a kérdésre egy másik tétel adja meg a választ, amelynek megfogalmazásához még egy fogalmat vezetünk be. Fő átlós mátrix minorok a kiskorúak a bal felső sarokban találhatók:
,
, 
, … , 
.
Tétel.Egy másodfokú alak akkor és csak akkor pozitív határozott, ha minden főátlós mollja pozitív.
Bizonyíték teljes matematikai indukciós módszerrel hajtjuk végre a számon n másodfokú alakváltozók f.
Az indukció hipotézise. Tegyük fel, hogy a kevesebb változót tartalmazó másodfokú formák esetében n az állítás helyes.
Tekintsük a másodfokú formát n változók. Gyűjtsd egy zárójelbe az összes olyan kifejezést, amely tartalmazza a -t. A fennmaradó tagok változókban másodfokú formát alkotnak. Az indukciós hipotézis szerint az állítás igaz rá.
Tegyük fel, hogy a másodfokú alak pozitív határozott. Ekkor a másodfokú alak is pozitív határozott. Ha feltételezzük, hogy ez nem így van, akkor van egy nem nulla változó értékkészlet 
, amelyekre 
és ennek megfelelően, 
, ami ellentmond annak, hogy a másodfokú alak pozitív határozott. Az indukciós hipotézis szerint egy másodfokú alak minden főátlós mollja pozitív, azaz. minden másodfokú formájú első fő minor f pozitívak. Másodfokú alak utolsó fő moll –
mátrixának meghatározója. Ez a determináns pozitív, hiszen előjele egybeesik normálformájának mátrixának előjelével, azaz. az identitásmátrix meghatározó előjelével.
Legyen a másodfokú alak összes főátló-mollja pozitív, majd a másodfokú alak összes főátló-mollja pozitív az egyenlőségből 
. Az indukciós hipotézis szerint a másodfokú alak pozitív határozott, tehát a változók egy nem degenerált lineáris transzformációja van, amely az alakot az új változók négyzetösszegének alakjára redukálja. Ez a lineáris transzformáció kiterjeszthető az összes változó nem degenerált lineáris transzformációjára a beállítással. A másodfokú formát ezzel a formává alakítva redukáljuk
A másodfokú forma fogalma. Másodfokú mátrix. Másodfokú forma kanonikus alakja. Lagrange módszer. A másodfokú forma normálalakja. Másodfokú alak rangsora, indexe és aláírása. Pozitív határozott másodfokú forma. Kvadrikus.
A másodfokú forma fogalma: függvény a vektor koordinátáiban egy másodfokú homogén polinom által adott vektortéren.
másodfokú forma -ból n ismeretlen 
összegnek nevezzük, amelynek minden tagja vagy az egyik ismeretlen négyzete, vagy két különböző ismeretlen szorzata.
Kvadratikus mátrix: A mátrixot az adott alapon másodfokú mátrixnak nevezzük. Ha a térkarakterisztika nem egyenlő 2-vel, akkor feltételezhetjük, hogy a másodfokú alak mátrixa szimmetrikus, azaz .
Írj fel egy másodfokú mátrixot:
Ennélfogva,
Vektormátrix formában a másodfokú alak a következő:
A , hol 
A másodfokú forma kanonikus formája: A másodfokú formát kanonikusnak nevezzük 
azaz
Bármilyen másodfokú forma lineáris transzformációkkal redukálható kanonikus formává. A gyakorlatban általában a következő módszereket alkalmazzák.
Lagrange módszer : a teljes négyzetek egymást követő kiválasztása. Például ha
Ezután hasonló eljárást hajtunk végre a másodfokú formával 
stb. Ha másodfokú formában minden van, kivéve 
majd egy előzetes átalakítás után a szóban forgó eljárásra redukálják a dolgot. Így, ha például akkor beállítjuk 
A másodfokú forma normál alakja: A normál másodfokú forma egy kanonikus másodfokú forma, amelyben minden együttható +1 vagy -1.
Másodfokú alak rangsora, indexe és aláírása: A másodfokú alak rangja A a mátrix rangjának nevezzük A. A másodfokú alakok rangja nem változik az ismeretlenek nem degenerált transzformációi során.
A negatív együtthatók számát negatív alakindexnek nevezzük.
A kanonikus formában lévő pozitív tagok számát a másodfokú forma pozitív tehetetlenségi indexének, a negatív tagok számát negatív indexnek nevezzük. A pozitív és negatív indexek közötti különbséget a másodfokú forma aláírásának nevezzük
Pozitív határozott másodfokú forma: Valódi kvadratikus forma 
pozitív-határozottnak (negatív-határozottnak) nevezzük, ha a változók bármely valós értékére, amely egyidejűleg nem egyenlő nullával
. (36)
Ebben az esetben a mátrixot pozitív határozottnak (negatív határozottnak) is nevezik.
A pozitív-határozott (negatív-határozott) formák osztálya a nemnegatív (illetve nem pozitív) formák osztályának része.
Quadok: négyes - n-dimenziós hiperfelület be n+1-dimenziós tér, egy másodfokú polinom nullák halmazaként definiálva. Ha megadja a koordinátákat ( x 1 , x 2 , x n+1 ) (euklideszi vagy affin térben), az általános másodfokú egyenlet alakja
Ez az egyenlet tömörebben átírható mátrixjelöléssel:
ahol x = ( x 1 , x 2 , x n+1 ) egy sorvektor, x T a transzponált vektor, K a méretmátrix ( n+1)×( n+1) (feltételezzük, hogy legalább egy eleme nem nulla), P egy sorvektor, és R egy állandó. Leggyakrabban a négyes számokat valós vagy komplex számok helyett tekintik. A definíció kiterjeszthető a projektív térben lévő négyzetekre, lásd alább.
Általánosabban, a polinomiális egyenletrendszer nullák halmazát algebrai változatnak nevezzük. Így a négyes egy (affin vagy projektív) algebrai másodfokú és 1-es kodimenziós változat.
Sík- és tértranszformációk.
Síktranszformáció meghatározása. A mozgás meghatározása. mozgási tulajdonságok. Kétféle mozgás: az első típusú mozgás és a második típusú mozgás. Példák mozgásra. A mozgás analitikus kifejezése. Síkmozgások osztályozása (fix pontok és invariáns egyenesek meglététől függően). Síkmozgások csoportja.
Síktranszformáció meghatározása: Definíció. A pontok közötti távolságot megőrző síktranszformációt nevezzük mozgalom(vagy elmozdulása). A síktranszformációt ún affin, ha bármely három ugyanazon az egyenesen fekvő pontot átveszi három, szintén ugyanazon az egyenesen fekvő pontba, és ugyanakkor megőrzi a három pont egyszerű összefüggését.
A mozgás meghatározása: Ez egy alaktranszformáció, amely megőrzi a pontok közötti távolságokat. Ha két figurát mozgással pontosan kombinálunk egymással, akkor ezek a figurák azonosak, egyenlőek.
Mozgás tulajdonságai: egy sík minden orientációmegőrző mozgása vagy párhuzamos transzláció vagy elforgatás; a sík minden orientációt megváltoztató mozgása vagy tengelyirányú szimmetria vagy csúszó szimmetria. Az egyenesen fekvő pontok mozgáskor átmennek egy egyenesen fekvő pontokba, és ezek kölcsönös elrendezésének sorrendje megmarad. Mozgáskor a félvonalak közötti szögek megmaradnak.
Kétféle mozgás: az első típusú mozgás és a második típusú mozgás: Az első típusú mozgások azok a mozdulatok, amelyek megőrzik egy bizonyos alakzat alapjainak tájolását. Folyamatos mozgásokkal valósíthatók meg.
A második típusú mozgások azok a mozgások, amelyek az alapok irányát az ellenkezőjére változtatják. Folyamatos mozgással nem valósíthatók meg.
Az első típusú mozgások példái az egyenes vonal körüli elfordítás és forgatás, a második típusú mozgások pedig a központi és tükörszimmetriák.
Tetszőleges számú első típusú mozgás összetétele az első típusú mozgás.
A második típusú páros számú mozgás összetétele az 1. típusú tétel, a páratlan számú 2. típusú mozgás összetétele pedig a 2. típusú tétel.
Példák mozgásra:Párhuzamos átvitel. Legyen a egy adott vektor. Az a vektorra való párhuzamos átvitel a sík önmagára való leképezése, amelyben minden M pont az M 1 pontra van leképezve, hogy az MM 1 vektor egyenlő az a vektorral.
A párhuzamos fordítás mozgás, mert a síkot önmagára leképezi, megőrzi a távolságokat. Vizuálisan ezt a mozgást úgy ábrázolhatjuk, mint a teljes sík eltolódását egy adott a vektor hosszának függvényében.
Fordulj. Jelöljünk ki egy O pontot a síkon ( forgóközpont) és állítsa be az α szöget ( forgásszög). A sík O pont körüli elforgatása az α szöggel a sík önmagára való leképezése, amelyben minden M pont az M 1 pontra van leképezve, hogy OM = OM 1 és a MOM 1 szög egyenlő α-val. Ebben az esetben az O pont a helyén marad, azaz önmagában jelenik meg, és az összes többi pont az O pont körül ugyanabban az irányban - az óramutató járásával megegyezően vagy azzal ellentétes - forog (az ábra az óramutató járásával ellentétes forgást mutat).
A fordulat mozgás, mert a sík önmagára való leképezése, amely megőrzi a távolságokat.
A mozgás analitikus kifejezése: az előkép koordinátái és a pont képe közötti analitikus kapcsolat alakja (1).
Síkmozgások osztályozása (fix pontok és invariáns vonalak jelenlététől függően): Definíció:
Egy síkban lévő pont akkor invariáns (rögzített), ha egy adott transzformáció során önmagává alakul.
Példa: Központi szimmetria esetén a szimmetriaközéppont pontja invariáns. Forduláskor a forgásközéppont invariáns. Axiális szimmetria esetén az egyenes invariáns - a szimmetriatengely az invariáns pontok egyenese.
Tétel: Ha a mozgásnak nincs invariáns pontja, akkor legalább egy invariáns iránya van.
Példa: Párhuzamos átvitel. Valójában az ezzel az iránnyal párhuzamos egyenesek mint egész alakzatok invariánsak, bár nem invariáns pontokból áll.
Tétel: Ha valamelyik sugár elmozdul, a sugár önmagába fordítódik, akkor ez a mozgás vagy azonos transzformáció, vagy szimmetria az adott sugarat tartalmazó egyeneshez képest.
Ezért az invariáns pontok vagy figurák jelenléte szerint lehetséges a mozgások osztályozása.
| Mozgás neve | Invariáns pontok | Változatlan vonalak |
| Az első típusú mozgás. | ||
| 1. - fordul | (középen) - 0 | Nem |
| 2. Identitás transzformáció | a sík összes pontja | mind egyenesen |
| 3. Központi szimmetria | pont 0 - középpont | a 0 ponton átmenő összes egyenes |
| 4. Párhuzamos átvitel | Nem | mind egyenesen |
| A második típusú mozgás. | ||
| 5. Tengelyszimmetria. | pontok halmaza | szimmetriatengely (egyenes) mind egyenes |
Repülőgép mozgás csoport: A geometriában fontos szerepet kapnak az önegybeesésből álló alakcsoportok. Ha - valamilyen alak a síkon (vagy a térben), akkor tekinthetjük a sík (vagy tér) mindazon mozgásainak halmazát, amelyekben az alak önmagába megy át.
Ez a készlet egy csoport. Például egy egyenlő oldalú háromszögnél a háromszöget magába vevő síkmozgások csoportja 6 elemből áll: egy pont körüli szögekkel történő elforgatásból és három egyenes körüli szimmetriából.
ábrán láthatók. 1 piros vonalakkal. Egy szabályos háromszög önegybeesési csoportjának elemei más módon is megadhatók. Ennek tisztázása érdekében számozzuk meg egy szabályos háromszög csúcsait 1, 2, 3 számokkal. feltételesen beírható a következő zárójelek egyikébe:
stb.
ahol az 1, 2, 3 számok azon csúcsok számát jelölik, amelyekbe a vizsgált mozgás eredményeként az 1, 2, 3 csúcsok átjutnak.
Projektív terek és modelljeik.
A projektív tér fogalma és a projektív tér modellje. A projektív geometria alapjai. Az O pont középpontjában álló vonalcsokor egy projektív síkmodell. projektív pontok. A kiterjesztett sík a projektív sík modellje. A kiterjesztett háromdimenziós affin vagy euklideszi tér egy projektív térmodell. Sík- és térbeli alakzatok képei párhuzamos kivitelben.
A projektív tér fogalma és a projektív tér modellje:
A mező feletti projektív tér egy adott mező feletti lineáris tér vonalaiból (egydimenziós altereiből) álló tér. Az egyenes tereket ún pontok projektív tér. Ez a meghatározás alkalmas egy tetszőleges testre történő általánosításra
Ha dimenziója van, akkor a projektív tér dimenzióját számnak nevezzük, magát a projektív teret pedig jelöljük és társítva nevezzük (ennek jelzésére a jelölést veszik át).
A dimenziós vektortérből a megfelelő projektív térbe való átmenetet ún projektivizálás terek.
A pontok homogén koordinátákkal írhatók le.
A projektív geometria alapjai: A projektív geometria a geometriának egy olyan ága, amely a projektív síkokat és tereket vizsgálja. A projektív geometria fő jellemzője a kettősség elve, amely kecses szimmetriát ad sok tervnek. A projektív geometria tanulmányozható tisztán geometriai szempontból, valamint analitikai (homogén koordinátákkal) és salgebrai szempontból, a projektív síkot egy mező feletti szerkezetnek tekintve. Gyakran és történelmileg a valódi projektív síkot euklideszi síkként kezelik egy "végtelen vonallal" kiegészítve.
Míg az ábrák tulajdonságai, amelyekkel az euklideszi geometria foglalkozik, azok metrikus(szögek, szakaszok, területek konkrét értékei), és az ábrák egyenértékűsége megegyezik azokkal egyezést(vagyis amikor az alakzatokat mozgással egymásba lehet fordítani a metrikus tulajdonságok megőrzése mellett), a geometriai alakzatoknak több "mélyebb" tulajdonsága van, amelyeket a mozgásnál általánosabb típusú transzformációk őriznek meg. A projektív geometria az osztály alatt invariáns alakzatok tulajdonságait vizsgálja projektív transzformációk, valamint maguk ezek az átalakulások.
A projektív geometria kiegészíti az euklideszi elméletet azzal, hogy gyönyörű és egyszerű megoldásokat kínál számos olyan problémára, amelyet a párhuzamos vonalak jelenléte bonyolít. A kúpszelvények projektív elmélete különösen egyszerű és elegáns.
A projektív geometriának három fő megközelítése van: a független axiomatizálás, az euklideszi geometriához való hozzáadás és a mező feletti struktúra.
Axiomatizálás
Egy projektív teret más axiómakészlettel is meghatározhatunk.
A Coxeter a következőket nyújtja:
1. Van egy egyenes, és egy pont nincs rajta.
2. Minden egyenesen legalább három pont van.
3. Két ponton keresztül pontosan egy egyenes húzható.
4. Ha A, B, C, És D különböző pontok és ABÉs CD akkor metszik egymást ACÉs BD metszik egymást.
5. Ha ABC egy sík, akkor legalább egy pont nincs a síkban ABC.
6. Két különböző sík legalább két pontban metszi egymást.
7. Egy teljes négyszög három átlós pontja nem kollineáris.
8. Ha három pont van egy egyenesen x x
A projektív síkot (a harmadik dimenzió nélkül) némileg eltérő axiómák határozzák meg:
1. Két ponton keresztül pontosan egy egyenes húzható.
2. Bármely két egyenes metszi egymást.
3. Négy pont van, amiből nincs három kollineáris.
4. A teljes négyszögek három átlós pontja nem kollineáris.
5. Ha három pont van egy egyenesen x invariánsak φ projektivitása alatt, akkor az összes pont on x invariánsak φ-hez képest.
6. Desargues-tétel: Ha két háromszög egy ponton keresztül perspektivikus, akkor egy egyenesen keresztül perspektivikus.
Egy harmadik dimenzió jelenlétében Desargues tétele az ideális pont és egyenes bevezetése nélkül is bebizonyítható.
Kiterjesztett sík - projektív sík modell: egy A3 affin térben vegyünk egy S(O) egyenes köteget, amelynek középpontja egy O pont és egy Π sík, amely nem megy át a köteg középpontján: O 6∈ Π. Az affin térben lévő vonalköteg a projektív sík modellje. Állítsuk be a Π sík ponthalmazának leképezését az S köteg vonalaira (A fenébe, imádkozz, ha megkaptad ezt a kérdést, elnézést!)
Kiterjesztett háromdimenziós affin vagy euklideszi tér - projektív térmodell:
Annak érdekében, hogy a leképezés szürjektív legyen, megismételjük a Π affin sík formális kiterjesztésének folyamatát a projektív síkra, Π, kiegészítve a Π síkot olyan helytelen pontokkal (M∞), hogy: ((M∞)) = P0(O). Mivel a leképezés során az S(O) síkköteg minden síkjának inverz képe egy egyenes a d síkon, nyilvánvaló, hogy a kiterjesztett sík összes helytelen pontjának halmaza: Π = Π ∩ (M∞), (M∞), a kiterjesztett sík d∞ nem megfelelő egyenese, amely a Π = 0 képének (∞ P = 0) képe. = Π0). (I.23) Állapodjunk meg abban, hogy itt és az alábbiakban a P0(O) = Π0 utolsó egyenlőséget ponthalmazok egyenlősége értelmében fogjuk érteni, de különböző struktúrákkal felruházva. Az affin síkot egy nem megfelelő vonallal kiegészítve biztosítottuk, hogy a leképezés (I.21) bijektív legyen a kiterjesztett sík összes pontjának halmazán:
Lapos és térbeli figurák képei párhuzamos kivitelben:
A sztereometriában a térbeli alakzatokat tanulmányozzák, de a rajzon lapos figurákként ábrázolják őket. Hogyan kell tehát egy térbeli alakot síkon ábrázolni? Általában a geometriában párhuzamos tervezést alkalmaznak erre. Legyen p valami sík, l- azt metsző egyenes (1. ábra). Egy tetszőleges ponton keresztül A, nem tartozik a vonalhoz l húzz egy vonalat párhuzamosan a vonallal l. Ennek az egyenesnek a p síkkal való metszéspontját a pont párhuzamos vetületének nevezzük A az egyenes irányába eső p síkra l. Jelöljük A". Ha a lényeg A sorhoz tartozik l, majd a párhuzamos vetítés A a p síkra az egyenes metszéspontjának tekintjük l síkkal p.
Így minden pont A a tér leképeződik a vetületére A" a p síkra. Ezt a megfelelést nevezzük a p síkra az egyenes irányában történő párhuzamos vetítésnek l.
Projektív transzformációk csoportja. Alkalmazás problémamegoldásra.
A sík projektív transzformációjának fogalma. Példák projektív síktranszformációkra. Projektív transzformációk tulajdonságai. Homológia, a homológia tulajdonságai. Projektív transzformációk csoportja.
A projektív síktranszformáció fogalma: A projektív transzformáció fogalma általánosítja a központi vetület fogalmát. Ha végrehajtjuk az α sík központi vetületét valamilyen α 1 síkra, akkor α 1 vetítését α 2 -re, α 2 vetítését α 3 -ra, ... és végül valamilyen α síkra. n ismét α 1 -en, akkor mindezen vetületek összetétele az α sík projektív transzformációja; egy ilyen lánc párhuzamos vetületeket tartalmazhat.
Példák projektív sík transzformációra: Egy kibővített sík projektív transzformációja a saját magára való egy-egy leképezése, amely megőrzi a pontok kollinearitását, vagy más szóval bármely egyenes képe egyenes. Bármely projektív transzformáció központi és párhuzamos vetületek láncolatának összetétele. Az affin transzformáció a projektív transzformáció speciális esete, amelyben a végtelenben lévő egyenes önmagába megy.
A projektív transzformációk tulajdonságai:
A projektív transzformáció során három, nem egy egyenesen lévő pont leképeződik három nem egy egyenesen lévő pontra.
Projektív transzformáció során a keret átmegy a keretre.
A projektív transzformáció során a vonal egyenesbe megy, a kéve kéve.
Homológia, homológia tulajdonságai:
Homológiának nevezzük egy olyan sík projektív transzformációját, amelyben invariáns pontokból álló vonal van, és így invariáns vonalakból álló ceruza.
1. A megfelelő nem egybeeső homológiapontokon átmenő egyenes invariáns egyenes;
2. A megfelelő nem egybeeső homológiapontokon átmenő egyenesek ugyanahhoz a ceruzához tartoznak, amelynek középpontja egy invariáns pont.
3. Egy pont, annak képe és a homológia középpontja ugyanazon az egyenesen fekszik.
Projektív transzformációk csoportja: tekintsük a P 2 projektív sík önmagára való projektív leképezését, vagyis ennek a síknak a projektív transzformációját (P 2 ’ = P 2).
Mint korábban, a P 2 projektív sík f 1 és f 2 projektív transzformációinak f összetétele az f 1 és f 2 transzformációk egymás utáni végrehajtásának eredménye: f = f 2 °f 1 .
1. Tétel: A P 2 projektív sík összes projektív transzformációjának H halmaza a projektív transzformációk összetétele alatti csoport.
Kvadratikus formák
másodfokú forma n változó f(x 1, x 2,...,x n)-ét összegnek nevezzük, amelynek minden tagja vagy valamelyik változó négyzete, vagy két különböző változó szorzata, valamilyen együtthatóval felvéve: f(x 1, x 2,...,x n) = (a ij = a ji).
Az ezekből az együtthatókból álló A mátrixot másodfokú alakmátrixnak nevezzük. Mindig szimmetrikus mátrix (azaz a főátlóra szimmetrikus mátrix, a ij = a ji).
A mátrix jelölésben a másodfokú alak az f(X) = X T AX formátumú, ahol
Valóban
Például írjuk fel a másodfokú formát mátrix alakban.
Ehhez egy másodfokú mátrixot találunk. Átlós elemei egyenlők a változók négyzeténél lévő együtthatókkal, a többi elem pedig a másodfokú forma megfelelő együtthatóinak felével. Ezért
Legyen az X változók mátrixoszlopa az Y mátrixoszlop nem degenerált lineáris transzformációjával, azaz. X = CY, ahol C egy nem degenerált n-rendű mátrix. Ezután a másodfokú forma
f(X) \u003d X T AX \u003d (CY) T A (CY) \u003d (Y T C T) A (CY) \u003d Y T (C T AC) Y.
Így egy nem degenerált C lineáris transzformáció során a másodfokú alak mátrixa a következő alakot ölti: A * = C T AC.
Például keressük meg az f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 másodfokú alakból lineáris transzformációval kapott f(y 1, y 2) másodfokú alakot.
A másodfokú formát ún kánoni(Van kanonikus nézet) ha minden együtthatója a ij = 0 i ≠ j esetén, azaz.
f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + ... + a nn x n 2 = .
Mátrixa átlós.
Tétel(a bizonyíték itt nincs megadva). Nem degenerált lineáris transzformáció segítségével bármely másodfokú forma kanonikus formává redukálható.
Például redukáljuk a kanonikus formára a másodfokú formát
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
Ehhez először válassza ki az x 1 változó teljes négyzetét:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 x 2 -.
Most kiválasztjuk az x 2 változó teljes négyzetét:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 - 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) - (5/100) x 3 2 \u003d
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 - (1/20) x 3 2.
Ezután az y 1 \u003d x 1 + x 2, y 2 \u003d x 2 - (1/10) x 3 és y 3 \u003d x 3 nem degenerált lineáris transzformáció ezt a másodfokú formát az f (y 1, y 2 \u003d x 2, u 0 -3 d 2 y -0 y 3 \u003d x 3) kanonikus alakra redukálja. (1/20) y 3 2.
Megjegyzendő, hogy a másodfokú formák kanonikus formája kétértelműen definiálható (ugyanaz a másodfokú forma többféleképpen redukálható a kanonikus formára). A különféle módszerekkel kapott kanonikus formák azonban számos közös tulajdonsággal rendelkeznek. Különösen a másodfokú alak pozitív (negatív) együtthatóival rendelkező tagok száma nem függ attól, hogy az alak hogyan redukálódik erre a formára (például a vizsgált példában mindig két negatív és egy pozitív együttható lesz). Ezt a tulajdonságot ún a másodfokú formák tehetetlenségi törvénye.
Ellenőrizzük ezt úgy, hogy ugyanazt a másodfokú formát más módon redukáljuk kanonikus formára. Kezdjük az átalakítást az x 2 változóval:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d - 3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 - 2 \u003
- 2 * x 2 ((1/6) x 3 + (2/3) x 1) + ((1/6) x 3 + (2/3) x 1) 2) - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d
\u003d -3 (x 2 - (1/6) x 3 - (2/3) x 1) 2 - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) \u003d - 2
-3y 2 2 + 2y 3 2, ahol y 1 \u003d - (2/3) x 1 + x 2 - (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 és y 3 \u003d x 1. Itt egy pozitív együttható 2 y 3-nál és két negatív együttható (-3) y 1-nél és y 2-nél (és egy másik módszerrel y 1-nél pozitív 2-es, y 2-nél pedig két negatív együttható - (-5), y 3-nál pedig (-1/20) kaptunk.
Azt is meg kell jegyezni, hogy egy másodfokú alakú mátrix rangja, ún a másodfokú forma rangja, megegyezik a kanonikus forma nullától eltérő együtthatóinak számával, és nem változik a lineáris transzformációk során.
Az f(X) másodfokú alakot nevezzük pozitívan (negatív) bizonyos, ha a változók összes olyan értékére, amely nem egyenlő egyidejűleg nullával, akkor pozitív, pl. f(X) > 0 (negatív, pl.
f(X)< 0).
Például az f 1 (X) \u003d x 1 2 + x 2 2 másodfokú alak pozitív határozott, mert a négyzetek összege, és az f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 másodfokú alak negatív határozott, mert azt jelenti, hogy f 2 (X) \u003d - (x 1 - x 2) 2-ként ábrázolható.
A legtöbb gyakorlati helyzetben valamivel nehezebb egy másodfokú alak előjel-határozottságát megállapítani, ezért erre a következő tételek valamelyikét használjuk (bizonyítások nélkül fogalmazzuk meg).
Tétel. Egy másodfokú forma akkor és csak akkor pozitív (negatív) határozott, ha mátrixának minden sajátértéke pozitív (negatív).
Tétel (Sylvester-kritérium). Egy másodfokú alak akkor és csak akkor pozitív határozott, ha ennek az alaknak a mátrixának minden fő minorja pozitív.
Major (sarok) moll Az A mátrix n-edik rendű k-edik rendjét a mátrix determinánsának nevezzük, amely az A () mátrix első k sorából és oszlopából áll.
Figyeljük meg, hogy a negatív-határozott másodfokú alakoknál a főmollok előjelei váltakoznak, az elsőrendű mollnak pedig negatívnak kell lennie.
Megvizsgáljuk például az f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 másodfokú alakot az előjel-határozottság szempontjából.
= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 \u003d 0; D \u003d 25 - 8 = 17; 
. Ezért a másodfokú forma pozitív határozott.
2. módszer. A mátrix első rendű főmollja A D 1 = a 11 = 2 > 0. A másodrendű főmoll D 2 = = 6 - 4 = 2 > 0. Ezért a Sylvester-kritérium szerint a másodfokú alak pozitív határozott.
Megvizsgálunk egy másik másodfokú alakot az előjel-meghatározásra, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.
1. módszer. Készítsünk А = másodfokú mátrixot. A karakterisztikus egyenlet alakja lesz 
= (-2 - l)*
*(-3 - l) - 4 \u003d (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 \u003d 0; D \u003d 25 - 8 = 17; 
. Ezért a másodfokú alak negatív határozott.
Négyzet alakú formák.
A formák jelentősége. Sylvester kritériuma
A „négyzet” jelző azonnal azt sugallja, hogy itt valami négyzethez (második fokozat) kapcsolódik, és hamarosan meg fogjuk tudni ezt a „valamit”, és azt, hogy mi az a forma. Azonnal kiderült :)
Üdvözöllek az új órámon, azonnali bemelegítésként pedig megnézzük a csíkos formát lineáris. Lineáris forma változók hívott homogén 1. fokú polinom:
- néhány konkrét szám *
(feltételezzük, hogy ezek közül legalább az egyik különbözik nullától), és olyan változók, amelyek tetszőleges értéket vehetnek fel.
* Ebben a témában csak megfontoljuk valós számok .
A "homogén" kifejezéssel már találkoztunk a kb homogén lineáris egyenletrendszerek, és ebben az esetben ez azt jelenti, hogy a polinomnak nincs hozzáadott állandója.
Például: 
– két változó lineáris alakja
Most az alak négyzetes. másodfokú forma változók hívott homogén 2. fokú polinom, amelynek minden tagját vagy a változó négyzetét tartalmazza, vagy kettős változók szorzata. Így például két változó másodfokú alakja a következő:
Figyelem! Ez egy szabványos bejegyzés, és nem kell rajta változtatni semmit! A „szörnyű” megjelenés ellenére itt minden egyszerű - az állandók dupla indexei jelzik, hogy mely változók szerepelnek egy vagy másik kifejezésben:
– ez a kifejezés a és a (négyzet) szorzatot tartalmazza;
- itt a munka;
- és itt a munka.
- Azonnal durva hibára számítok, amikor elveszítik az együttható "mínuszát", és nem veszik észre, hogy ez a kifejezésre vonatkozik:
Néha van egy "iskolai" változata a designnak a szellemben, de akkor csak néha. Egyébként vegye figyelembe, hogy az itt található állandók egyáltalán nem mondanak nekünk semmit, és ezért nehezebb megjegyezni a „könnyű jelölést”. Főleg, ha több változó van.
És három változó másodfokú alakja már hat tagot tartalmaz:
... miért szerepel a "két" szorzó a "vegyes" kifejezésben? Ez kényelmes, és hamarosan kiderül, miért.
Az általános képletet azonban felírjuk, kényelmes egy „lappal” elrendezni:
- alaposan tanulmányozd át az egyes sorokat - nincs ezzel semmi baj!
A másodfokú forma négyzetes változókkal rendelkező kifejezéseket és párszorzatú kifejezéseket tartalmaz (cm. kombinációk kombinatorikus képlete) . Semmi más - nincs "magányos x" és nincs hozzáadott állandó (akkor nem másodfokú alakot kapsz, hanem heterogén 2. fokú polinom).
Másodfokú alak mátrixjelölése
Az értékektől függően a figyelembe vett forma pozitív és negatív értéket is felvehet, és ugyanez vonatkozik bármely lineáris alakra - ha legalább az egyik együtthatója nem nulla, akkor pozitív vagy negatív is lehet (értékeitől függően).
Ezt a formát ún váltakozó. És ha minden átlátszó a lineáris formával, akkor a dolgok sokkal érdekesebbek a másodfokú formával:
Teljesen világos, hogy ez a forma bármilyen jel értékeit felveheti, így a másodfokú alak is lehet váltakozó.
Lehet, hogy nem:
– mindig, kivéve, ha mindkettő egyenlő nullával.
- bárkinek vektor nullát kivéve.
És általában véve, ha valamelyikre nem nulla vektor , , akkor a másodfokú alakot nevezzük pozitív határozott; ha akkor negatív határozott.
És minden rendben is lenne, de a másodfokú forma határozottsága csak egyszerű példákban látható, és ez a láthatóság már egy kis bonyodalommal elvész: 
– ?
Feltételezhetjük, hogy a forma pozitívan meghatározott, de valóban így van? Hirtelen vannak olyan értékek, amelyeknél kisebb, mint nulla?
Ezen a számlán, ott tétel: Ha mindenki sajátértékek a másodfokú mátrixok pozitívak * , akkor pozitívan definiált. Ha mindegyik negatív, akkor az negatív.
* Elméletileg bebizonyosodott, hogy egy valódi szimmetrikus mátrix összes sajátértéke érvényes
Írjuk fel a fenti forma mátrixát: 
és az egyenletből 
keressük meg őt sajátértékek:
Megoldjuk a régi jót másodfokú egyenlet:
, tehát az űrlap 
pozitívan definiált, azaz. bármely nem nulla érték esetén nagyobb, mint nulla.
Úgy tűnik, a megfontolt módszer működik, de van egy nagy DE. Már a „háromszor három” mátrix esetében a sajátértékek keresése hosszú és kellemetlen feladat; nagy valószínűséggel irracionális gyökökkel rendelkező 3. fokú polinomot kapsz.
Hogyan legyen? Van egy egyszerűbb út is!
Sylvester kritériuma
Nem, nem Sylvester Stallone :) Először is hadd emlékeztesselek, mire szögletes kiskorúak mátrixok. Ez meghatározó tényezők 
amely a bal felső sarkából "nő": 
az utolsó pedig pontosan egyenlő a mátrix determinánsával.
Most pedig valójában kritérium:
1) Másodfokú forma meghatározva pozitívan akkor és csak akkor, ha ÖSSZES szög-moll értéke nagyobb nullánál: .
2) Meghatározott másodfokú forma negatív akkor és csak akkor, ha szögmolljai előjelben váltakoznak, míg az 1. moll kisebb, mint nulla: , , ha páros vagy , ha páratlan.
Ha legalább egy szögletű moll ellentétes előjelű, akkor az űrlap jel-váltakozó. Ha a szögletes kiskorúak „az” előjelűek, de nullák vannak közöttük, akkor ez egy speciális eset, amit kicsit később elemzek, miután a gyakoribb példákra kattintunk.
Elemezzük a mátrix szögmolljait 
:
És ez azonnal azt mondja, hogy a forma nem negatívan meghatározott.
Következtetés: minden szög-moll nullánál nagyobb, tehát az alakzat 
pozitívan meghatározott.
Van különbség a sajátérték módszerrel? ;)
Ebből írjuk az alakmátrixot 1. példa:
első szögletes mollja és a második 
, amiből az következik, hogy a forma jel-váltakozó, azaz. értékétől függően pozitív és negatív értékeket is felvehet. Ez azonban annyira nyilvánvaló.
Vegyük a formát és a mátrixát innen 2. példa:
itt egyáltalán belátás nélkül nem érteni. De a Sylvester-kritériummal nem foglalkozunk:
, ezért a forma határozottan nem negatív.
, és határozottan nem pozitív. (mert minden szög minornak pozitívnak kell lennie).
Következtetés: a forma váltakozó.
Bemelegítési példák önmegoldáshoz:
4. példa
Vizsgálja meg a másodfokú alakokat az előjel-határozottság érdekében
A) 
Ezekben a példákban minden sima (lásd a lecke végén), de valójában egy ilyen feladat elvégzése Sylvester kritériuma nem biztos, hogy elégséges.
A lényeg az, hogy vannak "határesetek", mégpedig: ha van ilyen nem nulla vektor, akkor az alakzat definiálva van nem negatív, ha akkor nem pozitív. Ezek a formák rendelkeznek nem nulla vektorok, amelyekre .
Ide hozhatsz egy ilyen "gombos harmonikát":
Kiemelés teljes négyzet, azonnal látjuk nem negativitás forma: , ráadásul minden egyenlő koordinátájú vektornál egyenlő nullával, például: 
.
"Tükör" példa nem pozitív bizonyos formában:
és egy még triviálisabb példa:
– itt a forma egyenlő nullával bármely vektor esetén, ahol tetszőleges szám.
Hogyan lehet feltárni egy forma nem-negativitását vagy nem pozitív voltát?
Ehhez szükségünk van a koncepcióra jelentősebb kiskorúak
mátrixok. A fő-moll egy moll, amely olyan elemekből áll, amelyek azonos számú sorok és oszlopok metszéspontjában vannak. Tehát a mátrixnak két elsőrendű fő minorja van:
(az elem az 1. sor és az 1. oszlop metszéspontjában van);
(az elem a 2. sor és a 2. oszlop metszéspontjában van),
és egy fő 2. rendű moll: 
- az 1., 2. sor és 1., 2. oszlop elemeiből áll.
Mátrix "háromszor három" 
Hét fő kiskorú van, és itt már integetni kell a bicepszedet:
- három I. rendű kiskorú,
három másodrendű kiskorú: 
- az 1., 2. sor és 1., 2. oszlop elemeiből áll; 
- az 1., 3. sor és 1., 3. oszlop elemeiből áll; 
- a 2., 3. sor és 2., 3. oszlop elemeiből áll,
és egy 3. rendű minor: 
- az 1., 2., 3. sor és 1., 2. és 3. oszlop elemeiből áll.
Gyakorlat a megértéshez: írja le a mátrix összes fő minorját 
.
A lecke végén ellenőrizzük és folytatjuk.
Schwarzenegger-kritérium:
1) Nem nulla* másodfokú alak definiálva nem negatív akkor és csak akkor, ha az ÖSSZES fő kiskorú nem negatív(nullánál nagyobb vagy egyenlő).
* A nulla (degenerált) másodfokú alak minden együtthatója nullával egyenlő.
2) Nem nulla másodfokú forma definiált mátrixszal nem pozitív akkor és csak akkor, ha:
– I. rendű főkiskorúak nem pozitív(nullánál kisebb vagy egyenlő);
2. rendű fő kiskorúak nem negatív;
– III. rendű főkiskorúak nem pozitív(a váltakozás megkezdődött);
…
– sz. rendű dúr moll nem pozitív, ha páratlan ill nem negatív, ha páros.
Ha legalább egy kiskorú ellentétes előjelű, akkor a forma jel-váltakozó.
Nézzük meg, hogyan működik a kritérium a fenti példákban:
Készítsünk alakmátrixot, és Először számoljuk ki a szögletes minorokat – mi van ha pozitívan vagy negatívan definiált? 
A kapott értékek nem felelnek meg a Sylvester-kritériumnak, azonban a második kisebb nem negatív, és ez szükségessé teszi a 2. kritérium ellenőrzését (a 2. feltétel esetén nem teljesül automatikusan, azaz azonnal következtetés születik az űrlap jelváltoztatására).
I. rendű nagyobb kiskorúak:
- pozitívak
2. rendű dúr moll: 
- nem negatív.
Így MINDEN nagyobb minor nem negatív, tehát az űrlap nem negatív.
Írjuk fel az űrlapmátrixot 
, amelyre nyilvánvalóan a Sylvester-kritérium nem teljesül. De ellentétes előjeleket sem kaptunk (mert mindkét szögletű kiskorú egyenlő nullával). Ezért ellenőrizzük a nem-negativitás/nem-pozitivitás kritériumának teljesülését. I. rendű nagyobb kiskorúak:
- nem pozitív
2. rendű dúr moll: 
- nem negatív.
Így a Schwarzenegger-kritérium (2. pont) szerint a forma nem pozitívan kerül meghatározásra.
Most teljesen felfegyverkezve egy szórakoztatóbb problémát elemezünk:
5. példa
Vizsgálja meg a másodfokú alak jel-határozottságát
Ezt az űrlapot az "alfa" sorrend díszíti, amely bármely valós számmal egyenlő lehet. De ez csak szórakoztatóbb lesz döntsd el.
Először is írjuk fel az űrlapmátrixot, valószínűleg sokan alkalmazkodtak már szóban: on főátló az együtthatókat a négyzetekre, a szimmetrikus helyekre pedig a megfelelő "vegyes" termékek félegyütthatóit helyezzük:
Számítsuk ki az angular minorokat: 
A harmadik determinánst kiterjesztem a 3. sor mentén:
Ebben a részben a pozitív másodfokú formák egy speciális, de fontos osztályára fogunk összpontosítani.
3. definíció. Egy valós másodfokú formát nem negatívnak (nem pozitívnak) nevezünk, ha a változók bármely valós értékére
. (35)
Ebben az esetben az együtthatók szimmetrikus mátrixát pozitív félhatározottnak (negatív félhatározottnak) nevezzük.
4. definíció. Egy valós másodfokú formát pozitív-határozottnak (negatív-határozottnak) nevezzük, ha a változók bármely valós értékére, amely egyidejűleg nem egyenlő nullával
. (36)
Ebben az esetben a mátrixot pozitív határozottnak (negatív határozottnak) is nevezik.
A pozitív-határozott (negatív-határozott) formák osztálya a nemnegatív (illetve nem pozitív) formák osztályának része.
Legyen megadva egy nemnegatív alak. Független négyzetek összegeként ábrázoljuk:
. (37)
Ebben az ábrázolásban minden négyzetnek pozitívnak kell lennie:
. (38)
Valóban, ha lenne ilyen, akkor lehetne választani olyan értékeket, amelyekhez
De akkor a változók ezen értékei esetén az űrlap negatív értéket kap, ami a feltétel miatt lehetetlen. Nyilvánvalóan fordítva, a (37)-ből és a (38)-ból az következik, hogy a forma pozitív.
Így egy nemnegatív másodfokú formát az egyenlőségek jellemeznek.
Legyen most egy pozitív határozott forma. Aztán a nemnegatív forma is. Ezért a (37) formában ábrázolható, ahol mindegyik pozitív. A forma pozitív meghatározottságából következik, hogy . Valóban, abban az esetben választhatunk olyan értékeket, amelyek nem egyenlőek egyidejűleg nullával, amelyeknél minden eltűnne. De akkor a (37) alapján at , ami ellentmond a (36) feltételnek.
Könnyen belátható, hogy fordítva, ha a (37)-ben és mind pozitívak, akkor ez egy pozitív határozott forma.
Más szóval, egy nemnegatív forma akkor és csak akkor pozitív határozott, ha nem szinguláris.
A következő tétel ad egy kritériumot egy forma pozitív meghatározottságára olyan egyenlőtlenségek formájában, amelyeknek az alak együtthatóinak teljesülniük kell. Ebben az esetben az előző szakaszokban a mátrix egymást követő fő minorjaira vonatkozó jelölést használjuk:
.
3. Tétel. Ahhoz, hogy egy másodfokú alak pozitív határozott legyen, szükséges és elégséges, hogy az egyenlőtlenségek
Bizonyíték. A feltételek (39) elégségessége közvetlenül következik a (28) Jacobi-képletből. A feltételek (39) szükségességét a következőképpen állapítjuk meg. A forma pozitív meghatározottságából következik a "csonka" formák pozitív meghatározottsága
.
De akkor ezeknek a formáknak nem egyesszámúaknak kell lenniük, azaz.
Most lehetőségünk van a Jacobi-formula (28) használatára (for ). Mivel a képlet jobb oldalán minden négyzetnek pozitívnak kell lennie, akkor
Ez egyenlőtlenségeket von maga után (39). A tétel bizonyítást nyert.
Mivel a mátrix bármely főmollja a változók megfelelő átszámozásával a bal felső sarokba helyezhető, így
Következmény. Pozitív határozott másodfokú formában az együtthatómátrix összes fő minorja pozitív:
Megjegyzés. Az egymást követő fő kiskorúak nem-negativitásából
nem követi a forma nem-negativitását. Valóban, a forma
,
ahol 
, megfelel a feltételeknek, de nem nem negatív.
Van azonban a következő
4. Tétel. Ahhoz, hogy egy másodfokú alak ne legyen negatív, szükséges és elegendő, hogy az együtthatómátrixának minden fő minorja ne legyen negatív:
Bizonyíték. Vezessünk be egy segédformát, amely nem pozitív, szükséges és elégséges, hogy az egyenlőtlenségek
kapcsolódó cikkek
