Чьи штаны на все стороны равны. Сокровище геометрии
Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля.
- - тройки целых положительных чисел х, у,z, удовлетворяющих уравнению x2+у 2=z2...
Математическая энциклопедия
- - тройки таких натуральных чисел, что треугольник, длины сторон к-рого пропорциональны этим числам, является прямоугольным, напр. тройка чисел: 3, 4, 5...
Естествознание. Энциклопедический словарь
- - см. Ракета спасательная...
Морской словарь
- - тройки натуральных чисел таких, что треугольник, длины сторон которого пропорциональны этим числам, является прямоугольным...
Большая Советская энциклопедия
- - mil. Неизм. Выражение, используемое при перечислении или противопоставлении двух фактов, явлений, обстоятельств...
Учебный фразеологический словарь
- - Из романа-антиутопии «Скотный двор» английского писателя Джорджа Оруэлла...
- - Впервые встречается в сатире «Дневник либерала в Петербурге» Михаила Евграфовича Салтыкова-Щедрина, который так образно описал двойственную, трусливую позицию российских либералов - своих...
Словарь крылатых слов и выражений
- - Говорится в случае, когда собеседник долго и невнятно пытался что-то сообщить, загромождая основную мысль второстепенными деталями...
Словарь народной фразеологии
- - Число пуговиц известно. Почему же хую тесно? - о штанах и мужском половом органе. . Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах...
Живая речь. Словарь разговорных выражений
- - Ср. Нет бессмертия души, так нет и добродетели, "значит, все позволено"... Соблазнительная теория подлецам... Хвастунишка, а суть-то вся: с одной стороны, нельзя не признаться, а с другой - нельзя не сознаться...
Толково-фразеологический словарь Михельсона
- - Пиѳагоровы штаны иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны... Салтыковъ. Пестрыя письма...
- - Съ одной стороны - съ другой стороны. Ср. Нѣтъ безсмертія души, такъ нѣтъ и добродѣтели, «значитъ, все позволено»... Соблазнительная теорія подлецамъ.....
Толково-фразеологический словарь Михельсона (ориг. орф.)
- - Шуточное название теоремы Пифагора, возникшее в силу того, что построенные на сторонах прямоугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов...
- - С ОДНОЙ СТОРОНЫ… С ДРУГОЙ СТОРОНЫ. Книжн...
Фразеологический словарь русского литературного языка
- - См. ЗВАНИЯ -...
В.И. Даль. Пословицы русского народа
- - Жарг. шк. Шутл. Пифагор. ...
Большой словарь русских поговорок
"Пифагоровы штаны во все стороны равны" в книгах
11. Пифагоровы штаны
Из книги Фридл автора Макарова Елена Григорьевна11. Пифагоровы штаны Моя хорошая девочка!Прежде всего – самая горячая благодарность за Дворжака; он очень интересен, не так уж легко читается, но я ему очень рада. Я тебе напишу подробнее, когда прочту несколько глав.Ты не представляешь, какую радость доставляет мне твой
III «Не все ли места равны?»
Из книги Батюшков автора Сергеева-Клятис Анна ЮрьевнаIII «Не все ли места равны?» В конце поста, не дождавшись Пасхи, которая в 1815 году приходилась на 18 апреля, Батюшков на Страстной седмице выехал из Петербурга в имение отца Даниловское. Однако до этого произошло еще одно событие, о котором нет упоминаний в письмах Батюшкова,
Пифагоровы штаны
Из книги От добермана до хулигана. Из имен собственных в нарицательные автора Блау Марк ГригорьевичПифагоровы штаны О том, что «пифагоровы штаны во все стороны равны», знали еще дореволюционные гимназисты, они-то и сочинили эту стихотворную шпаргалку. Да что там гимназисты! Наверное, уже великому Ломоносову, изучавшему геометрию в своей Славяно-греко-латинской
1.16. Обеспечительные меры как со стороны налоговых органов, так и со стороны налогоплательщиков
Из книги Налоговые проверки. Как с достоинством выдержать визит инспекторов автора Семенихин Виталий Викторович1.16. Обеспечительные меры как со стороны налоговых органов, так и со стороны налогоплательщиков Налогоплательщики редко соглашаются с выводами налоговых органов, сделанными по результатам налоговых проверок. И при этом большинство споров в судах разрешается в пользу
Перед кредитом все равны
Из книги Деньги. Кредит. Банки: конспект лекций автора Шевчук Денис АлександровичПеред кредитом все равны Официальная история неотложного кредитования в Америке ведет отсчет с 1968 года, когда там был принят Закон о потребительском кредите. В частности, он устанавливает справедливые правила предоставления ссуды, верхние пределы ставок, правила
SWOT-анализ (сильные стороны, слабые стороны, возможности, угрозы)
Из книги Треннинг. Настольная книга тренера автора Торн КейSWOT-анализ (сильные стороны, слабые стороны, возможности, угрозы) Этот способ - дополнение структуры «мозговому штурму». Разделите лист флип-чарта на четыре части и озаглавьте их: сильные стороны, слабые стороны, возможности, угрозы.Группа может анализировать бизнес,
Не все покупатели равны
Из книги Как работать по четыре часа в неделю автора Феррис ТимотиНе все покупатели равны Как только вы достигнете третьего этапа и приток средств станет более-менее установившимся, пора оценить состав ваших покупателей и прополоть эту грядку. Все на свете делится на хорошее и плохое: хорошими и плохими бывают еда, фильмы, секс. Вот и
Глава VII «Пифагоровы штаны» - открытие ассиро-вавилонских математиков
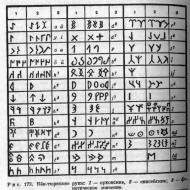
Из книги Когда заговорила клинопись автора Матвеев Константин ПетровичГлава VII «Пифагоровы штаны» - открытие ассиро-вавилонских математиков Математика у ассирийцев и вавилонян, так же как и астрономия, была необходима прежде всего в практической жизни - при строительстве домов, дворцов, дорог, составлении календарей, проведении каналов,
«Под маской все чины равны»
Из книги Петербургские арабески автора Аспидов Альберт Павлович«Под маской все чины равны» Среди новогодних покупок - елочных игрушек и прочего - может оказаться и маска. Надев ее, мы сразу же становимся другими - как в волшебной сказке. А кто не хочет хоть раз в году прикоснуться к волшебству - к его радостным и безобидным сторонам,
Пифагоровы числа
Из книги Большая Советская Энциклопедия (ПИ) автора БСЭВсе равны, но некоторые равны более других
Из книги Энциклопедический словарь крылатых слов и выражений автора Серов Вадим ВасильевичВсе равны, но некоторые равны более других Из романа-антиутопии «Скотный двор» (1945) английского писателя Джорджа Оруэлла (псевдоним Эрика Блэра, 1903-1950). Животные некой фермы однажды свергли своего жестокого хозяина и установили республику, провозгласив принцип: «Все
Участие в переговорах в качестве стороны или ассистента стороны
Из книги Хрестоматия альтернативного разрешения споров автора Коллектив авторовУчастие в переговорах в качестве стороны или ассистента стороны Еще одной из форм переговоров, вышедших из медиации, является участие медиатора совместно со стороной (или без нее) в переговорах в качестве представителя стороны.Такой метод принципиально отличается от
Силы были равны
Из книги Великая война не окончена. Итоги Первой Мировой автора Млечин Леонид МихайловичСилы были равны Никто не предполагал, что война затянется. Но тщательно разработанные Генштабами планы рухнули в первые же месяцы. Силы противостоящих блоков оказались примерно равными. Расцвет новой боевой техники множил число жертв, но не позволял сокрушить врага и
Все животные равны, но некоторые более равны, чем другие
Из книги Фашизофрения автора Сысоев Геннадий БорисовичВсе животные равны, но некоторые более равны, чем другие И наконец, хотелось бы вспомнить людей, которые думают, будто Косово может стать каким-то там прецедентом. Мол, если населению Косова «мировое сообщество» (т.е. США и ЕС) предоставит право самому решить свою судьбу на
Почти равны
Из книги Литературная Газета 6282 (№ 27 2010) автора Литературная ГазетаПочти равны Клуб 12 стульев Почти равны ИРОНИЧЕСКАЯ ПРОЗА Смерть зашла к одному бедняку. А тот глуховатый был. Так нормальный, но чуть-чуть глуховатый… И видел плохо. Почти ничего не видел. – Ой, к нам гости! Проходите, пожалуйста. Смерть говорит: – Погоди радоваться,
Потенциал к творчеству обычно приписывают гуманитарным дисциплинам, естественно научным оставляя анализ, практический подход и сухой язык формул и цифр. Математику к гуманитарным предметам никак не отнесешь. Но без творчеств в «царице всех наук» далеко не уедешь – об этом людям известно с давних пор. Со времен Пифагора, например.
Школьные учебники, к сожалению, обычно не объясняют, что в математике важно не только зубрить теоремы, аксиомы и формулы. Важно понимать и чувствовать ее фундаментальные принципы. И при этом попробовать освободить свой ум от штампов и азбучных истин – только в таких условиях рождаются все великие открытия.
К таким открытиям можно отнести и то, которое сегодня мы знаем как теорему Пифагора. С его помощью мы попробуем показать, что математика не только может, но и должна быть увлекательной. И что это приключение подходит не только ботаникам в толстых очках, а всем, кто крепок умом и силен духом.
Из истории вопроса
Строго говоря, хоть теорема и называется «теоремой Пифагора», сам Пифагор ее не открывал. Прямоугольный треугольник и его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал.
Также сегодня известно, что задачи о прямоугольном треугольнике встречаются в египетских источниках времен фараона Аменемхета I, на вавилонских глиняных табличках периода правления царя Хаммурапи, в древнеиндийском трактате «Сульва сутра» и древнекитайском сочинении «Чжоу-би суань цзинь».
Как видите, теорема Пифагора занимала умы математиков с древнейших времен. Подтверждением служит и около 367 разнообразных доказательств, существующих сегодня. В этом с ней не может тягаться ни одна другая теорема. Среди знаменитых авторов доказательств можно вспомнить Леонардо да Винчи и двадцатого президента США Джеймса Гарфилда. Все это говорит о чрезвычайной важности этой теоремы для математики: из нее выводится или так или иначе с нею связано большинство теорем геометрии.
Доказательства теоремы Пифагора
В школьных учебниках в основном приводят алгебраические доказательства. Но суть теоремы в геометрии, так что давайте рассмотрим в первую очередь те доказателства знаменитой теоремы, которые опираются на эту науку.
Доказательство 1
Для самого простого доказательства теоремы Пифагора для прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.
Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» можно проиллюстрировать следующим чертежом:
Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны» :

Доказательство 2
Этот метод сочетает в себе алгебру и геометрию и может рассматриваться как вариант древнеиндийского доказательства математика Бхаскари.
Постройте прямоугольный треугольник со сторонами a, b и c (рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов, – (a+b) . В каждом из квадратов выполните построения, как на рисунках 2 и 3.
В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b .
Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c .
Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b) .
Записав все это, имеем: a 2 +b 2 =(a+b) 2 – 2ab . Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a 2 +b 2 = a 2 +b 2 . При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c 2 . Т.е. a 2 +b 2 =c 2 – вы доказали теорему Пифагора.

Доказательство 3
Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».
Но мы разберем это доказательство более подробно:

Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с . Катеты треугольника назовем а и b . В соответствии с чертежом сторона внутреннего квадрата это (a-b) .
Используйте формулу площади квадрата S=c 2 , чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b) 2 2+4*1\2*a*b .
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c 2 =(a-b) 2 +4*1\2*a*b . В результате решения вы получите формулу теоремы Пифагора c 2 =a 2 +b 2 . Теорема доказана.
Доказательство 4
Это любопытное древнекитайское доказательство получило название «Стул невесты» - из-за похожей на стул фигуры, которая получается в результате всех построений:


В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.
Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a .
Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c 2 =a 2 +b 2 .
Доказательство 5
Это еще один способ найти решение для теоремы Пифагора, опираясь на геометрию. Называется он «Метод Гарфилда».
Постройте прямоугольный треугольник АВС . Нам надо доказать, что ВС 2 =АС 2 +АВ 2 .
Для этого продолжите катет АС и постройте отрезок CD , который равен катету АВ . Опустите перпендикулярный AD отрезок ED . Отрезки ED и АС равны. Соедините точки Е и В , а также Е и С и получите чертеж, как на рисунке ниже:

Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ , является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD , АС=ED и ВС=СЕ – это позволит нам упростить запись и не перегружать ее. Итак, S ABED =2*1/2(AB*AC)+1/2ВС 2 .
При этом очевидно, что ABED – это трапеция. Поэтому вычисляем ее площадь по формуле: S ABED =(DE+AB)*1/2AD . Для наших вычислений удобней и наглядней представить отрезок AD как сумму отрезков АС и CD .
Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC 2 =(DE+AB)*1/2(AC+CD) . Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC 2 =1/2(АВ+АС) 2 . А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC 2 =1/2АС 2 +2*1/2(АВ*АС)+1/2АВ 2 . Закончив все преобразования, получим именно то, что нам и надо: ВС 2 =АС 2 +АВ 2 . Мы доказали теорему.
Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.
Пару слов о Пифагоровых тройках
Этот вопрос мало или вообще не изучается в школьной программе. А между тем он является очень интересным и имеет большое значение в геометрии. Пифагоровы тройки применяются для решения многих математических задач. Представление о них может пригодиться вам в дальнейшем образовании.
Так что же такое Пифагоровы тройки? Так называют натуральные числа, собранные по трое, сумма квадратов двух из которых равна третьему числу в квадрате.
Пифагоровы тройки могут быть:
- примитивными (все три числа – взаимно простые);
- не примитивными (если каждое число тройки умножить на одно и то же число, получится новая тройка, которая не является примитивной).
Еще до нашей эры древних египтян завораживала мания чисел Пифагоровых троек: в задачах они рассматривали прямоугольный треугольник со сторонами 3,4 и 5 единиц. К слову, любой треугольник, стороны которого равны числам из пифагоровой тройки, по умолчанию является прямоугольным.
Примеры Пифагоровых троек: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) и т.д.
Практическое применение теоремы
Теорема Пифагора находит применение не только в математике, но и в архитектуре и строительстве, астрономии и даже литературе.
Сначала про строительство: теорема Пифагора находит в нем широкое применение в задачах разного уровня сложности. Например, посмотрите на окно в романском стиле:

Обозначим ширину окна как b , тогда радиус большой полуокружности можно обозначить как R и выразить через b: R=b/2 . Радиус меньших полуокружностей также выразим через b: r=b/4 . В этой задаче нас интересует радиус внутренней окружности окна (назовем его p ).
Теорема Пифагора как раз и пригодиться, чтобы вычислить р . Для этого используем прямоугольный треугольник, который на рисунке обозначен пунктиром. Гипотенуза треугольника состоит из двух радиусов: b/4+p . Один катет представляет собой радиус b/4 , другой b/2-p . Используя теорему Пифагора, запишем: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2 . Далее раскроем скобки и получим b 2 /16+ bp/2+p 2 =b 2 /16+b 2 /4-bp+p 2 . Преобразуем это выражение в bp/2=b 2 /4-bp . А затем разделим все члены на b , приведем подобные, чтобы получить 3/2*p=b/4 . И в итоге найдем, что p=b/6 – что нам и требовалось.
С помощью теоремы можно вычислить длину стропила для двускатной крыши. Определить, какой высоты вышка мобильной связи нужна, чтобы сигнал достигал определенного населенного пункта. И даже устойчиво установить новогоднюю елку на городской площади. Как видите, эта теорема живет не только на страницах учебников, но и часто бывает полезна в реальной жизни.
Что касается литературы, то теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:
Свет истины рассеется не скоро,
Но, воссияв, рассеется навряд
И, как тысячелетия назад,
Не вызовет сомнения и спора.
Мудрейшие, когда коснется взора
Свет истины, богов благодарят;
И сто быков, заколоты, лежат –
Ответный дар счастливца Пифагора.
С тех пор быки отчаянно ревут:
Навеки всполошило бычье племя
Событие, помянутое тут.
Им кажется: вот-вот настанет время,
И сызнова их в жертву принесут
Какой-нибудь великой теореме.
(перевод Виктора Топорова)
А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый».
А еще в книге «Приключения Электроника» автор устами учителя математики Таратара говорит: «Главное в математике – движение мысли, новые идеи». Именно этот творческий полет мысли порождает теорема Пифагора – не зря у нее столько разнообразных доказательств. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.
Заключение
Эта статья создана, чтобы вы могли заглянуть за пределы школьной программы по математике и узнать не только те доказательства теоремы Пифагора, которые приведены в учебниках «Геометрия 7-9» (Л.С. Атанасян, В.Н. Руденко) и «Геометрия 7-11» (А.В. Погорелов), но и другие любопытные способы доказать знаменитую теорему. А также увидеть примеры, как теорема Пифагора может применяться в обычной жизни.
Во-первых, эта информация позволит вам претендовать на более высокие баллы на уроках математики – сведения по предмету из дополнительных источников всегда высоко оцениваются.
Во-вторых, нам хотелось помочь вам прочувствовать, насколько математика интересная наука. Убедиться на конкретных примерах, что в ней всегда есть место творчеству. Мы надеемся, что теорема Пифагора и эта статья вдохновят вас на самостоятельные поиски и волнующие открытия в математике и других науках.
Расскажите нам в комментариях, показались ли вам приведенные в статье доказательства интересными. Пригодились ли вам эти сведения в учебе. Напишите нам, что думаете о теореме Пифагора и этой статье – нам будет приятно обсудить все это с вами.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
«Пифагоровы штаны – на все стороны равны.
Чтобы это доказать, надо снять и показать».
Этот стишок известен всем со средней школы, с тех самых пор, когда на уроке геометрии мы изучали знаменитую теорему Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Хотя сам Пифагор никогда не носил штанов – в те времена греки их не носили. Кто же такой Пифагор?
Пифагор Самосский от лат. Pythagoras, пифийский вещатель (570-490 гг.до н.э.) – древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.
Среди противоречивых учений своих учителей Пифагор искал живой связи, синтеза единого великого целого. Он поставил себе цель - найти путь ведущий к свету истины, то есть познать жизнь в единстве. С этой целью Пифагор посетил весь древний мир. Он считал, что должен расширить и без того уже широкой кругозор, изучая все религии, доктрины и культы. Он жил среди раввинов и много узнал о тайных традициях Моисея, законодателя Израиля. Затем посетил Египет, где был посвящен в Мистерии Адониса, и, сумев пересечь долину Евфрата, он находился долго у халдеев, чтобы перенять их секретную мудрость. Пифагор посетил Азию и Африку, в том числе Индостан и Вавилон. В Вавилоне он изучил знания магов.
Заслугой пифагорейцев было выдвижение мысли о количественных закономерностях развития мира, что содействовало развитию математических, физических, астрономических и географических знаний. В основе вещей лежит Число, учил Пифагор, познать мир – значит познать управляющие им числа. Изучая числа, пифагорейцы разработали числовые отношения и нашли их во всех областях человеческой деятельности. Пифагор учил тайно и не оставил после себя письменных трудов. Пифагор придавал большое значение числу. Его философские взгляды в значительной мере обусловлены математическими представлениями. Он говорил: «Всё есть число», «все вещи суть числа», выделяя, таким образом, одну сторону в понимании мира, а именно, его измеряемость числовым выражением. Пифагор считал, что число владеет всеми вещами, в том числе и нравственными, и духовными качествами. Он учил (согласно Аристотелю): «Справедливость… есть число, помноженное само на себя». Он полагал, что в каждом предмете, помимо его изменчивых состояний, существует неизменное бытие, некая неизменная субстанция. Это и есть число. Отсюда основная идея пифагореизма: число – основа всего сущего. Пифагорейцы видели в числе и в математических отношениях объяснение скрытого смысла явлений, законов природы. По мнению Пифагора, объекты мысли более реальны, чем объекты чувственного познания, так как числа имеют вневременную природу, т.е. вечны. Они – некая реальность, стоящая выше реальности вещей. Пифагор говорит, что все свойства предмета могут быть уничтожены, или могут измениться, кроме одного лишь числового свойства. Это свойство – Единица. Единица – это бытие вещей, неуничтожимая и неразложимая, неизменное. Раздробите любой предмет на мельчайшие частицы – каждая частица будет одна. Утверждая, что числовое бытие есть единственно неизменное бытие, Пифагор пришел к выводу, что все предметы есть суть копии чисел.
Единица есть абсолютное число Единица обладает вечностью. Единице не надо находиться ни в каком отношении к чему-либо иному. Она существует сама по себе. Два есть только отношение одного к одному. Все числа есть лишь
числовые отношения Единицы, её модификации. А все формы бытия есть лишь определённые стороны бесконечности, а значит и Единицы. Первоначальное Один заключает в себе все числа, следовательно, заключает в себе элементы всего мира. Предметы – это реальные проявления абстрактного бытия. Пифагор был первым, кто обозначил космос со всеми находящимися в нем вещами, как порядок, который устанавливается числом. Этот порядок доступен разуму, осознаётся им, что позволяет совершенно по-новому видеть мир.
Процесс познания мира, по Пифагору, есть процесс познания управляющих им чисел. Космос после Пифагора стал рассматриваться как упорядоченное числом мироздания.
Пифагор учил, что душа человека бессмертна. Ему принадлежит идея о переселении душ. Он считал, что всё происходящее в мире снова и снова повторяется через определённые периоды времени, а души умерших через какое-то время вселяются в других. Душа, как число представляет собой Единицу, т.е. душа совершенна по существу. Но всякое совершенство, поскольку оно приходит в движение, обращается в несовершенство, хотя и стремится обрести вновь свое прежнее совершенное состояние. Несовершенством Пифагор называл отклонение от Единицы; поэтому Два считалось проклятом числом. Душа в человеке пребывает в состоянии сравнительного несовершенства. Она состоит из трёх элементов: разум, ум, страсть. Но если умом и страстями обладают и животные, то разумом (рассудком) наделён только человек. Какая-либо из этих трёх сторон в человеке может возобладать, и тогда человек становится по преимуществу или разумным, или здравомыслящим, или же чувственным. Соответственно он оказывается или философом, или обыкновенным человеком, или животным.
Однако вернёмся к числам. Да действительно числа являются абстрактным проявлением основного философского закона Вселенной – Единства Противоположностей.
Примечание. Абстракция служит базой для процессов обобщения и образования понятий. Она – необходимое условие категоризации. Ею формируются обобщённые образы реальности, позволяющие выделить значимые для определённой деятельности связи и отношения объектов.
Единство Противоположностей Вселенной состоят из Формы и Содержания, Форма является количественной категорией, а Содержание качественной категорией. Естественно, что числа выражают в абстракции количественную и качественную категории. Отсюда сложение (вычитание) чисел это количественная составляющая абстракции Форм, а умножение (деление) – это качественная составляющая абстракции Содержания. Числа абстракции Форм и Содержания находятся в неразрывной связи Единства Противоположностей.
Попробуем произвести математические операции, над числами установив неразрывную связь Формы и Содержания.
Так рассмотрим числовой ряд.
1,2,3,4,5,6,7,8,9 . 1+2= 3 (3) 4+5=9 (9)… (6) 7+8=15 -1+5=6 (9). Далее 10 – (1+0) + 11 (1+1) = (1+2= 3) - 12 –(1+2=3) (3) 13-(1+3= 4) + 14 –(1+4=5) = (4+5= 9) (9) …15 –(1+5=6) (6) … 16- (1+6=7) + 17 – (1+7 =8) (7+8=15) – (1+5= 6) … (18) – (1+8=9) (9). 19 – (1+9= 10) (1) -20 – (2+0=2) (1+2=3) 21 –(2+1=3) (3) – 22- (2+2= 4) 23-(2+3=5) (4+5=9) (9) 24- (2+4=6) 25 – (2+5=7) 26 – (2+6= 8) – 7+ 8= 15 (1+5=6) (6) И т.д.
Отсюда мы наблюдаем циклическое преобразование Форм, которому соответствует цикл Содержания –1-й –цикл - 3-9-6 - 6-9-3 2-й цикл – 3-9- 6 -6-9-3 и т.д.
6
9 9
3
Циклы отображают выворот тора Вселенной, где Противоположностями чисел абстакции Форм и Содержания являются 3 и 6, где 3 определяет Сжатие, а 6 - Растяжение. Компромиссом для их взаимодействия является число 9.
Далее 1,2,3,4,5,6,7,8,9 . 1х2=2 (3) 4х5=20 (2+0=2) (6) 7х8=56 (5+6=11 1+1= 2) (9) и т.д.
Цикл выглядит так 2-(3)-2-(6)- 2- (9)… где 2 является составляющим элементом цикла 3-6-9.
Далее таблица умножения:
2х1=2
2х2=4
(2+4=6)
2х3=6
2х4=8
2х5=10
(8+1+0 = 9)
2х6=12
(1+2=3)
2х7=14
2х8=16
(1+4+1+6=12;1+2=3)
2х9=18
(1+8=9)
Цикл -6,6- 9- 3,3 – 9.
3х1=3
3х2=6
3х3=9
3х4=12 (1+2=3)
3х5=15 (1+5=6)
3х6=18 (1+8=9)
3х7=21 (2+1=3)
3х8=24 (2+4=6)
3х9=27 (2+7=9)
Цикл 3-6-9; 3-6-9; 3-6-9.
4х1=4
4х2=8 (4+8=12 1+2=3)
4х3=12 (1+2=3)
4х4=16
4х5=20 (1+6+2+0= 9)
4х6=24 (2+4=6)
4х7=28
4х8= 32 (2+8+3+2= 15 1+5=6)
4х9=36 (3+6=9)
Цикл 3,3 – 9 - 6,6 - 9.
5х1=5
5х2=10 (5+1+0=6)
5х3=15 (1+5=6)
5х4=20
5х5=25 (2+0+2+5=9)
5х6=30 (3+0=3)
5х7=35
5х8=40 (3+5+4+0= 12 1+2=3)
5х9=45 (4+5=9)
Цикл -6,6 – 9 - 3,3- 9.
6х1= 6
6х2=12 (1+2=3)
6х3=18 (1+8=9)
6х4=24 (2+4=6)
6х5=30 (3+0=3)
6х6=36 (3+6=9)
6х7=42 (4+2=6)
6х8=48 (4+8=12 1+2=3)
6х9=54 (5+4=9)
Цикл – 3-9-6; 3-9-6; 3-9.
7х1=7
7х2=14 (7+1+4= 12 1+2=3)
7х3=21 (2+1=3)
7х4=28
7х5=35 (2+8+3+5=18 1+8=9)
7х6=42 (4+2=6)
7х7=49
7х8=56 (4+9+5+6=24 2+4=6)
7х9=63 (6+3=9)
Цикл – 3,3 – 9 – 6,6 – 9.
8х1= 8
8х2=16 (8+1+6= 15 1+5=6.
8х3=24 (2+4=6)
8х4=32
8х5=40 (3+2+4+0 =9)
8х6=48 (4+8=12 1+2=3)
8х7=56
8х8=64 (5+6+6+4= 21 2+1=3)
8х9=72 (7+2=9)
Цикл -6,6 – 9 – 3,3 – 9.
9х1=9
9х2= 18 (1+8=9)
9х3= 27 (2+7=9)
9х4=36 (3+6=9)
9х5=45 (4+5= 9)
9х6=54 (5+4=9)
9х7=63 (6+3=9)
9х8=72 (7+2=9)
9х9=81 (8+1=9).
Цикл – 9-9-9-9-9-9-9-9-9.
Числа качественной категории Содержания – 3-6-9, указывают на ядро атома с разным количеством нейтронов, а количественной категории указывают на количество электронов атома. Химические элемент – это ядра, массы которых кратные 9, а кратные – 3 и 6 являются изотопами.
Примечание. Изотоп (от греч. «равный», «одинаковый» и «место») – разновидности атомов и ядер одного химического элемента с разным количеством нейтронов в ядре. Химический элемент – это совокупность атомов с одинаковыми зарядами ядра. Изотопы-разновидности атомов химического элемента с одинаковым зарядом ядра, но разным массовым числом.
Все действительные предметы состоят из атомов, а атомы определяются числами.
Поэтому естественно, что Пифагор был убеждён, что числа есть действительные предметы, а не простые символы. Число – это определённое состояние материальных предметов, сущность вещи. И в этом Пифагор был прав.
В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.
Краткий обзор биографии
Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.
Пифагор - философ, математик, мыслитель родом из Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.
Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.
Рождение теоремы
В юности Пифагор переехал с в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.
Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.
Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.
Теорема Пифагора
Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90 о, сумма квадратов катетов равна квадрату гипотенузы».
Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.
Способ первый
Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.
Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.
Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.
На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в) 2 . Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.
Поэтому площадь равна: 4*0,5ав+с 2 =2ав+с 2
Отсюда (а+в) 2 =2ав+с 2
И, следовательно, с 2 =а 2 +в 2
Теорема доказана.
Способ два: подобные треугольники
Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника - среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 о.
Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:
АС=√АВ*АД, СВ=√АВ*ДВ.
Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.
АС 2 =АВ*АД и СВ 2 =АВ*ДВ
Теперь нужно сложить получившиеся неравенства.
АС 2 + СВ 2 =АВ*(АД*ДВ), где АД+ДВ=АВ
Получается, что:
АС 2 + СВ 2 =АВ*АВ
И, следовательно:
АС 2 + СВ 2 =АВ 2

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.
Еще одна методика расчетов
Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.
В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.
Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:
S авс * с 2 - S авд *в 2 =S авд *а 2 - S всд *а 2
S авс *(с 2 -в 2)=а 2 *(S авд -S всд)
с 2 -в 2 =а 2
с 2 =а 2 +в 2
Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.
Самый простой способ доказать теорему Пифагора. Отзывы
Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а 2 +в 2 =с 2 , будет видно наглядно.
Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС - равнобедренный.
Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.
К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую - из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.
Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».
Доказательство Дж. Гарфилда
Джеймс Гарфилд - двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.
В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.
Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.
Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=а+в/2 * (а+в)
Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:
S=ав/2 *2 + с 2 /2
Теперь необходимо уравнять два исходных выражения
2ав/2 + с/2=(а+в) 2 /2
с 2 =а 2 +в 2
О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?
Практическое применение теоремы Пифагора
К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.
На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.
Связь теоремы и астрономии
Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия - это научная сфера, в которой широко используется теорема Пифагора.
Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l . А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем t . И скорость луча - c . Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.
Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t").
А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:
Если представить, что точки света С и В, а также космический лайнер - это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.
Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.
Радиус передачи мобильного сигнала
Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!
Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.
Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.
АВ (высота вышки) = х;
ВС (радиус передачи сигнала) = 200 км;
ОС (радиус земного шара) = 6380 км;
ОВ=ОА+АВОВ=r+х
Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту
Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.
Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.
Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка - 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.
При идеальных габаритах шкафа проверим действие теоремы Пифагора:
АС=√АВ 2 +√ВС 2
АС=√2474 2 +800 2 =2600 мм - все сходится.
Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:
АС=√2505 2 +√800 2 =2629 мм.
Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.
Теорема Пифагора всем известна со школьной поры. Выдающийся математик доказал великую гипотезу, которой в настоящее время пользуются многие люди. Звучит правило так: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. За многие десятилетия ни один математик не сумел переспорить данное правило. Ведь Пифагор долго шел к своей цели, чтобы в результате чертежи имели место в повседневной жизни.
- Небольшой стих к данной теореме, который придумали вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагоровы штаны во все стороны равны» . Это двустрочье отложилось в памяти у многих людей – по сей день стихотворение вспоминают при вычислениях.
- Данная теорема получила название «Пифагоровы штаны» вследствие того, что при черчении по середине получался прямоугольный треугольник, по бокам которого располагались квадраты . С виду данное черчение напоминало штаны – отсюда и название гипотезы.
- Пифагор гордился разработанной теоремой, ведь данная гипотеза отличается от ею подобных максимальным количеством доказательств . Важно: уравнение было занесено в книгу рекордов Гиннесса вследствие 370 правдивых доказательств.
- Гипотезу доказывало огромное количество математиков и профессоров из разных стран многими способами . Английский математик Джонс вскоре оглашения гипотезы доказал ее при помощи дифференциального уравнения.
- В настоящее время никому неизвестно доказательство теоремы самим Пифагором . Факты о доказательствах математика сегодня не известны никому. Считается, что доказательство чертежей Евклидом - это и есть доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы.
- Нынешние ученые обнаружили, что великий математик был не первым, кто открыл данную гипотезу . Уравнение было известно еще задолго до открытия Пифагором. Данный математик сумел лишь воссоединить гипотезу.
- Пифагор не давал уравнению название «Теорема Пифагора» . Это название закрепилось после «громкого двустрочья». Математик лишь хотел, чтобы его старания и открытия узнал весь мир и пользовался ими.
- Мориц Кантор - великий крупнейший математик нашел и разглядел на древнем папирусе записи с чертежами . Вскоре после этого Кантор понял, что данная теорема была известна египтянам еще 2300 лет до нашей эры. Только тогда ею никто не воспользовался и не стал пытаться доказать.
- Нынешние ученые считают, что гипотеза была известна еще в 8 веке до нашей эры . Индийские ученые того времени обнаружили приблизительное вычисление гипотенузы треугольника, наделенного прямыми углами. Правда в то время никто не смог доказать наверняка уравнение по приблизительным вычислениям.
- Великий математик Бартель Ван дер Варден после доказательства гипотезы заключил важный вывод : «Заслуга греческого математика считается не открытием направления и геометрии, а лишь ее обоснованием. В руках Пифагора были вычислительные формулы, которые основывались на предположениях, неточных вычислениях и смутных представлениях. Однако выдающемуся ученому удалось превратить из в точную науку».
- Известный стихотворец сказал, что в день открытия своего чертежа он воздвиг быкам славную жертву . Именно после открытия гипотезы пошли слухи, что жертвоприношение ста быков «пошло странствовать по страницам книг и изданий». Остряки по сей день шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что не Пифагор придумал стихотворение про штаны, дабы доказать выдвинутые им чертежи: во времена жизни великого математика штанов еще не было . Они были придуманы через несколько десятилетий.
- Пекка, Лейбниц и еще несколько ученых пытались доказать ранее известную теорему, однако это никому не удавалось .
- Название чертежей «теорема Пифагора» означает «убеждение речью» . Так переводится слово Пифагор, которое взял математик в качестве псевдонима.
- Размышления Пифагора о собственном правиле: секрет сущего на земле кроется в цифрах . Ведь математик, опираясь на собственную гипотезу, изучил свойства чисел, выявил четность и нечетность, создал пропорции.
Мы надеемся Вам понравилась подборка с картинками - Интересные факты о теореме Пифагора: узнаем новое об известной теореме (15 фото) онлайн хорошего качества. Оставьте пожалуйста ваше мнение в комментариях! Нам важно каждое мнение.