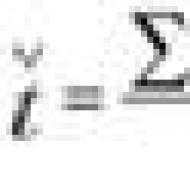Notacja macierzowa formy kwadratowej ma postać. Pozytywnie określone formy kwadratowe

Pozytywnie określone formy kwadratowe

Definicja. Forma kwadratowa od N nazywa się nieznany pozytywnie określony, jeśli jego ranga jest równa dodatniemu indeksowi bezwładności i jest równa liczbie niewiadomych.

Twierdzenie. Forma kwadratowa jest dodatnio określona wtedy i tylko wtedy, gdy przyjmuje wartości dodatnie na dowolnym niezerowym zbiorze wartości zmiennych.

Dowód. Niech forma kwadratowa będzie niezdegenerowaną liniową transformacją niewiadomych

wróciło do normy

.

Dla dowolnego niezerowego zestawu wartości zmiennych przynajmniej jedna z liczb różne od zera, tj. . Udowodniono konieczność twierdzenia.

Załóżmy, że forma kwadratowa przyjmuje wartości dodatnie na dowolnym niezerowym zbiorze zmiennych, ale jej indeks bezwładności jest dodatni. Przez niezdegenerowaną transformację liniową niewiadomych

Przywróćmy to do normy. Bez utraty ogólności możemy założyć, że w tej postaci normalnej kwadrat ostatniej zmiennej albo jest nieobecny, albo wchodzi do niej ze znakiem minus, tj. , gdzie lub . Załóżmy, że jest to niezerowy zbiór wartości zmiennych, otrzymany w wyniku rozwiązania układu równań liniowych

W systemie tym liczba równań jest równa liczbie zmiennych, a wyznacznik układu jest różny od zera. Zgodnie z twierdzeniem Cramera, system ma unikalne rozwiązanie i jest niezerowe. Do tego zestawu. Sprzeczność z warunkiem. Dochodzimy do sprzeczności z założeniem, co dowodzi wystarczalności twierdzenia.

Korzystając z tego kryterium, nie można określić na podstawie współczynników, czy forma kwadratowa jest dodatnio określona. Odpowiedź na to pytanie daje inne twierdzenie, dla sformułowania którego wprowadzamy jeszcze jedno pojęcie. Główne drugorzędne macierze diagonalne to nieletni znajdują się w lewym górnym rogu:

, , , … , .

Twierdzenie.Forma kwadratowa jest dodatnio określona wtedy i tylko wtedy, gdy wszystkie jej główne drugorzędne przekątne są dodatnie.

Dowód przeprowadzimy metodą pełnej indukcji matematycznej na liczbie N zmienne postaci kwadratowej F.

Hipoteza indukcji. Załóżmy, że dla form kwadratowych z mniejszą liczbą zmiennych N stwierdzenie jest poprawne.

Rozważ formę kwadratową z N zmienne. Zbierz w jednym nawiasie wszystkie terminy zawierające . Pozostałe terminy tworzą formę kwadratową w zmiennych. Na mocy hipotezy indukcyjnej stwierdzenie to jest dla niego prawdziwe.

Załóżmy, że forma kwadratowa jest dodatnio określona. Wtedy postać kwadratowa jest również dodatnio określona. Jeśli założymy, że tak nie jest, to istnieje niezerowy zbiór wartości zmiennych , dla którego i odpowiednio, , co jest sprzeczne z faktem, że forma kwadratowa jest dodatnio określona. Zgodnie z hipotezą indukcyjną wszystkie główne drugorzędne przekątne formy kwadratowej są dodatnie, tj. wszystkie pierwsze główne drobne formy kwadratowej F są pozytywne. Ostatni główny minor formy kwadratowej – jest wyznacznikiem jego macierzy. Wyznacznik ten jest dodatni, gdyż jego znak pokrywa się ze znakiem macierzy postaci normalnej, tj. ze znakiem wyznacznika macierzy tożsamości.

Niech wszystkie główne przekątne drugorzędne formy kwadratowej będą dodatnie.Wtedy wszystkie główne przekątne drugorzędne formy kwadratowej będą dodatnie z równości . Zgodnie z hipotezą indukcyjną forma kwadratowa jest dodatnio określona, ​​więc istnieje niezdegenerowana liniowa transformacja zmiennych, która redukuje formę do postaci sumy kwadratów nowych zmiennych. Ta transformacja liniowa może zostać rozszerzona na niezdegenerowaną transformację liniową wszystkich zmiennych przez ustawienie . Forma kwadratowa jest zredukowana przez to przekształcenie do formy

Pojęcie formy kwadratowej. Macierz formy kwadratowej. Postać kanoniczna formy kwadratowej. Metoda Lagrange'a. Postać normalna formy kwadratowej. Ranga, indeks i sygnatura formy kwadratowej. Pozytywnie określona forma kwadratowa. Kwadryk.

Pojęcie formy kwadratowej: funkcja na przestrzeni wektorowej określona przez jednorodny wielomian drugiego stopnia we współrzędnych wektora.

forma kwadratowa od N nieznany nazywa się sumą, której każdy wyraz jest albo kwadratem jednej z tych niewiadomych, albo iloczynem dwóch różnych niewiadomych.

Macierz kwadratowa: Macierz nazywana jest macierzą postaci kwadratowej w danej bazie. Jeśli charakterystyka pola nie jest równa 2, możemy założyć, że macierz postaci kwadratowej jest symetryczna, czyli .

Napisz macierz postaci kwadratowej:

Stąd,

W postaci wektorowo-macierzowej forma kwadratowa to:

A. gdzie

Postać kanoniczna formy kwadratowej: Forma kwadratowa nazywana jest kanoniczną, jeśli wszystkie tj.

Każdą formę kwadratową można sprowadzić do postaci kanonicznej za pomocą przekształceń liniowych. W praktyce zwykle stosuje się następujące metody.

Metoda Lagrange'a : kolejny wybór pełnych kwadratów. Na przykład, jeśli

Następnie podobna procedura jest wykonywana z formą kwadratową itd. Jeśli w formie kwadratowej wszystko oprócz jest następnie po wstępnym przekształceniu sprawa sprowadza się do rozpatrywanej procedury. Tak więc, jeśli na przykład, to ustawiamy

Postać normalna formy kwadratowej to: Normalna postać kwadratowa to kanoniczna postać kwadratowa, w której wszystkie współczynniki są równe +1 lub -1.

Ranga, indeks i sygnatura formy kwadratowej: Ranga formy kwadratowej A nazywamy rzędem macierzy A. Ranga formy kwadratowej nie zmienia się przy niezdegenerowanych przekształceniach niewiadomych.

Liczba ujemnych współczynników nazywana jest ujemnym wskaźnikiem kształtu.

Liczba wyrazów dodatnich w postaci kanonicznej nazywana jest dodatnim indeksem bezwładności postaci kwadratowej, liczba wyrazów ujemnych nazywana jest indeksem ujemnym. Różnica między indeksami dodatnimi i ujemnymi nazywana jest sygnaturą formy kwadratowej

Pozytywnie określona forma kwadratowa: Prawdziwa forma kwadratowa nazywa się dodatnio-określonym (określonym ujemnie), jeśli dla dowolnych rzeczywistych wartości zmiennych, które nie są jednocześnie równe zeru

. (36)

W tym przypadku macierz jest również nazywana dodatnio określoną (ujemnie określoną).

Klasa form dodatnio-określonych (negatywno-określonych) należy do klasy form nienegatywnych (odpowiednio niepozytywnych).

Quady: Kwadryptyk - N-wymiarowa hiperpowierzchnia w N Przestrzeń +1-wymiarowa, zdefiniowana jako zbiór zer wielomianu drugiego stopnia. Jeśli wpiszesz współrzędne ( X 1 , X 2 , x rz+1 ) (w przestrzeni euklidesowej lub afinicznej) ogólne równanie kwadratowe ma postać

To równanie można zapisać bardziej zwięźle w notacji macierzowej:

gdzie x = ( X 1 , X 2 , x rz+1 ) jest wektorem wierszowym, X T jest transponowanym wektorem, Q jest macierzą rozmiarów ( N+1)×( N+1) (zakłada się, że co najmniej jeden z jej elementów jest różny od zera), P jest wektorem wierszowym i R jest stałą. Najczęściej kwadryki są rozpatrywane w stosunku do liczb rzeczywistych lub zespolonych. Definicję można rozszerzyć na kwadryki w przestrzeni rzutowej, patrz poniżej.

Mówiąc bardziej ogólnie, zbiór zer układu równań wielomianowych jest znany jako rozmaitość algebraiczna. Zatem kwadryka jest (afiniczną lub rzutową) rozmaitością algebraiczną drugiego stopnia i współwymiaru 1.

Przekształcenia płaszczyznowe i przestrzenne.

Definicja transformacji płaszczyzny. Definicja ruchu. właściwości ruchu. Dwa rodzaje ruchów: ruch pierwszego rodzaju i ruch drugiego rodzaju. Przykłady ruchu. Analityczne wyrażenie ruchu. Klasyfikacja ruchów płaskich (w zależności od obecności punktów stałych i linii niezmienniczych). Grupa ruchów płaskich.

Definicja transformacji płaszczyzny: Definicja. Nazywa się transformację płaszczyzny, która zachowuje odległość między punktami ruch(lub przemieszczenie) samolotu. Nazywa się transformację płaszczyzny afiniczny, jeśli przenosi dowolne trzy punkty leżące na tej samej prostej do trzech punktów leżących również na tej samej prostej i jednocześnie zachowuje prostą relację trzech punktów.

Definicja ruchu: Jest to transformacja kształtu, która zachowuje odległości między punktami. Jeśli dwie figury są dokładnie połączone ze sobą za pomocą ruchu, to te figury są takie same, równe.

Właściwości ruchu: każdy ruch płaszczyzny zachowujący orientację jest albo translacją równoległą, albo obrotem; każdy ruch płaszczyzny zmieniający orientację jest albo symetrią osiową, albo symetrią ślizgową. Punkty leżące na linii prostej podczas ruchu przechodzą w punkty leżące na linii prostej, a kolejność ich wzajemnego ułożenia jest zachowana. Podczas przesuwania kąty między półprostymi są zachowywane.

Dwa rodzaje ruchów: ruch pierwszego rodzaju i ruch drugiego rodzaju: Ruchy pierwszego rodzaju to ruchy, które zachowują orientację podstaw określonej figury. Można je realizować ciągłymi ruchami.

Ruchy drugiego rodzaju to ruchy, które zmieniają orientację podstaw na przeciwną. Nie można ich zrealizować za pomocą ciągłych ruchów.

Przykładami ruchów pierwszego rodzaju są ruchy translacyjne i obrotowe wokół linii prostej, a ruchy drugiego rodzaju to symetrie centralne i lustrzane.

Złożenie dowolnej liczby ruchów pierwszego rodzaju jest ruchem pierwszego rodzaju.

Złożenie parzystej liczby ruchów drugiego rodzaju jest ruchem pierwszego rodzaju, a złożenie nieparzystej liczby ruchów drugiego rodzaju jest ruchem drugiego rodzaju.

Przykłady ruchu:Transfer równoległy. Niech a będzie danym wektorem. Przeniesienie równoległe do wektora a jest odwzorowaniem płaszczyzny na samą siebie, w którym każdy punkt M jest odwzorowany na punkt M1, tak że wektor MM1 jest równy wektorowi a.

Translacja równoległa jest ruchem, ponieważ jest odwzorowaniem płaszczyzny na siebie, z zachowaniem odległości. Wizualnie ruch ten można przedstawić jako przesunięcie całej płaszczyzny w kierunku danego wektora a o jego długość.

Zakręt . Wyznaczmy punkt O na płaszczyźnie ( centrum tokarskie) i ustaw kąt α ( kąt obrotu). Obrót płaszczyzny wokół punktu O o kąt α jest odwzorowaniem płaszczyzny na siebie, w którym każdy punkt M jest odwzorowany na punkt M 1, czyli OM = OM 1 i kąt MOM 1 jest równy α. W takim przypadku punkt O pozostaje na swoim miejscu, tj. Jest wyświetlany sam w sobie, a wszystkie inne punkty obracają się wokół punktu O w tym samym kierunku - zgodnie z ruchem wskazówek zegara lub przeciwnie do ruchu wskazówek zegara (rysunek pokazuje obrót w kierunku przeciwnym do ruchu wskazówek zegara).

Zwrot jest ruchem, ponieważ jest odwzorowaniem płaszczyzny na siebie, co zachowuje odległości.

Analityczna ekspresja ruchu: związek analityczny między współrzędnymi preobrazu a obrazem punktu ma postać (1).

Klasyfikacja ruchów płaskich (w zależności od obecności punktów stałych i linii niezmienniczych): Definicja:

Punkt na płaszczyźnie jest niezmienny (stały), jeżeli przy danej transformacji przekształca się w siebie.

Przykład: w przypadku symetrii centralnej punkt środka symetrii jest niezmienny. Podczas skręcania punkt środka obrotu jest niezmienny. Przy symetrii osiowej prosta jest niezmienna - osią symetrii jest linia niezmiennych punktów.

Twierdzenie: Jeśli ruch nie ma niezmiennego punktu, to ma co najmniej jeden niezmienny kierunek.

Przykład: Transfer równoległy. Rzeczywiście, linie równoległe do tego kierunku są niezmienne jako figura jako całość, chociaż nie składa się ona z niezmiennych punktów.

Twierdzenie: Jeżeli jakiś promień się porusza, to promień przechodzi w siebie, to ruch ten jest albo identyczną transformacją, albo symetrią względem prostej zawierającej dany promień.

Dlatego, zgodnie z obecnością niezmiennych punktów lub figur, możliwe jest klasyfikowanie ruchów.

Nazwa ruchu	Punkty niezmienne	Linie niezmienne
Ruch pierwszego rodzaju.
1. - obróć	(środek) - 0	NIE
2. Transformacja tożsamości	wszystkie punkty płaszczyzny	wszystko prosto
3. Centralna symetria	punkt 0 - środek	wszystkie proste przechodzące przez punkt 0
4. Transfer równoległy	NIE	wszystko prosto
Ruch drugiego rodzaju.
5. Symetria osiowa.	zestaw punktów	oś symetrii (prosta) cała prosta

Grupa ruchu samolotu: W geometrii ważną rolę odgrywają samozbieżne grupy figur. Jeśli - jakaś figura na płaszczyźnie (lub w przestrzeni), to możemy rozważyć zbiór wszystkich tych ruchów płaszczyzny (lub przestrzeni), w których figura przechodzi w siebie.

Ten zestaw to grupa. Na przykład w przypadku trójkąta równobocznego grupa ruchów płaskich, które obejmują trójkąt, składa się z 6 elementów: obrotów o kąt wokół punktu i symetrii wokół trzech prostych.

Są one pokazane na ryc. 1 z czerwonymi liniami. Elementy grupy samozbieżności trójkąta foremnego można określić w inny sposób. Aby to wyjaśnić, ponumerujmy wierzchołki trójkąta foremnego liczbami 1, 2, 3. można warunkowo wprowadzić w postaci jednego z tych nawiasów:

itp.

gdzie liczby 1, 2, 3 oznaczają numery tych wierzchołków, do których przechodzą wierzchołki 1, 2, 3 w wyniku rozważanego ruchu.

Przestrzenie rzutowe i ich modele.

Pojęcie przestrzeni rzutowej i model przestrzeni rzutowej. Podstawowe fakty geometrii rzutowej. Pęczek linii wyśrodkowany w punkcie O jest rzutowym modelem płaszczyzny. punkty projekcyjne. Płaszczyzna rozszerzona jest modelem płaszczyzny rzutowej. Rozszerzona trójwymiarowa przestrzeń afiniczna lub euklidesowa jest modelem przestrzeni rzutowej. Obrazy figur płaskich i przestrzennych w układzie równoległym.

Pojęcie przestrzeni rzutowej i model przestrzeni rzutowej:

Przestrzeń rzutowa nad polem to przestrzeń składająca się z linii (jednowymiarowych podprzestrzeni) pewnej przestrzeni liniowej nad danym polem. Proste przestrzenie są nazywane kropki przestrzeń rzutowa. Ta definicja nadaje się do uogólnienia na dowolne ciało

Jeśli ma wymiar , to wymiar przestrzeni rzutowej jest nazywany liczbą , a sama przestrzeń rzutowa jest oznaczona i nazywana powiązaną (aby to zaznaczyć, przyjmuje się notację).

Nazywa się przejście z przestrzeni wektorowej wymiaru do odpowiedniej przestrzeni rzutowej projekcja spacje.

Punkty można opisać za pomocą jednorodnych współrzędnych.

Podstawowe fakty geometrii rzutowej: Geometria rzutowa to gałąź geometrii, która bada rzutowe płaszczyzny i przestrzenie. Główną cechą geometrii rzutowej jest zasada dualności, która dodaje wielu projektom wdzięcznej symetrii. Geometrię rzutową można badać zarówno z czysto geometrycznego punktu widzenia, jak i analitycznego (przy użyciu jednorodnych współrzędnych) i salgebraicznego punktu widzenia, uznając płaszczyznę rzutową za strukturę nad polem. Często i historycznie rzeczywista płaszczyzna rzutowa jest traktowana jako płaszczyzna euklidesowa z dodatkiem „linii w nieskończoności”.

Natomiast właściwości figur, którymi zajmuje się geometria euklidesowa, są metryczny(konkretne wartości kątów, odcinków, pól), a równoważność figur jest im równoważna stosowność(tj. gdy figury mogą być przekładane na siebie za pomocą ruchu przy zachowaniu właściwości metrycznych), istnieją bardziej „głębsze” właściwości figur geometrycznych, które są zachowywane przez przekształcenia bardziej ogólnego typu niż ruch. Geometria rzutowa bada właściwości figur, które są niezmienne w ramach klasy przekształcenia rzutowe, a także same te przekształcenia.

Geometria rzutowa uzupełnia euklidesową, dostarczając pięknych i prostych rozwiązań wielu problemów skomplikowanych przez obecność linii równoległych. Rzutowa teoria przekrojów stożkowych jest szczególnie prosta i elegancka.

Istnieją trzy główne podejścia do geometrii rzutowej: niezależna aksjomatyzacja, dodatek do geometrii euklidesowej i struktura na polu.

Aksjomatyzacja

Przestrzeń rzutową można zdefiniować za pomocą innego zestawu aksjomatów.

Firma Coxeter zapewnia:

1. Jest linia i nie ma na niej punktu.

2. Na każdej linii są co najmniej trzy punkty.

3. Przez dwa punkty można poprowadzić dokładnie jedną linię prostą.

4. Jeśli A, B, C, I D różne punkty i AB I płyta CD przecinać się, w takim razie AC I BD przecinać.

5. Jeśli ABC jest płaszczyzną, to przynajmniej jeden punkt nie leży na płaszczyźnie ABC.

6. Dwie odrębne płaszczyzny przecinają się w co najmniej dwóch punktach.

7. Trzy przekątne pełnego czworoboku nie są współliniowe.

8. Jeśli na linii prostej są trzy punkty X X

Płaszczyzna rzutowa (bez trzeciego wymiaru) jest zdefiniowana przez nieco inne aksjomaty:

1. Przez dwa punkty można poprowadzić dokładnie jedną linię prostą.

2. Przecinają się dowolne dwie proste.

3. Istnieją cztery punkty, z których nie ma trzech współliniowych.

4. Trzy przekątne pełnych czworoboków nie są współliniowe.

5. Jeśli na linii prostej leżą trzy punkty X są niezmienne przy rzutowaniu φ, a następnie wszystkie punkty na X są niezmienne względem φ.

6. Twierdzenie Desarguesa: Jeśli dwa trójkąty są perspektywiczne przez punkt, to są perspektywiczne przez prostą.

W obecności trzeciego wymiaru twierdzenie Desarguesa można udowodnić bez wprowadzania idealnego punktu i prostej.

Płaszczyzna rozszerzona - model płaszczyzny rzutowej: w przestrzeni afinicznej A3 weź wiązkę prostych S(O) ze środkiem w punkcie O i płaszczyznę Π nieprzechodzącą przez środek wiązki: O 6∈ Π. Wiązka linii w przestrzeni afinicznej jest modelem płaszczyzny rzutowej. Ustawmy odwzorowanie zbioru punktów płaszczyzny Π na zbiór linii wiązki S (Cholera, módl się, jeśli masz to pytanie, przepraszam)

Rozszerzona trójwymiarowa przestrzeń afiniczna lub euklidesowa - model przestrzeni rzutowej:

Aby odwzorowanie było suriekcyjne, powtarzamy proces formalnego przedłużania płaszczyzny afinicznej Π do płaszczyzny rzutowej Π, uzupełniając płaszczyznę Π o zbiór punktów niewłaściwych (M∞) takich, że: ((M∞)) = P0(O). Ponieważ w odwzorowaniu obrazem odwrotnym każdej płaszczyzny wiązki płaszczyzn S(O) jest prosta na płaszczyźnie d, jest oczywiste, że zbiór wszystkich punktów niewłaściwych płaszczyzny rozciągniętej: Π = Π ∩ (M∞) , (M∞), jest linią niewłaściwą d∞ płaszczyzny rozciągniętej, która jest odwrotnym obrazem płaszczyzny osobliwej Π0: (d∞) = P0(O) (= Π0). (I.23) Umówmy się, że tutaj i poniżej ostatnią równość P0(O) = Π0 będziemy rozumieć w sensie równości zbiorów punktów, ale obdarzonych różnymi strukturami. Uzupełniając płaszczyznę afiniczną o prostą niewłaściwą, zapewniliśmy, że odwzorowanie (I.21) stanie się bijekcją na zbiorze wszystkich punktów płaszczyzny rozszerzonej:

Obrazy płaskich i przestrzennych postaci w układzie równoległym:

W stereometrii badane są figury przestrzenne, ale na rysunku są one przedstawiane jako figury płaskie. Jak zatem przedstawić figurę przestrzenną na płaszczyźnie? Zwykle w geometrii stosuje się do tego projektowanie równoległe. Niech p będzie pewną płaszczyzną, l- przecinającą ją linię prostą (rys. 1). Przez dowolny punkt A, nie należący do linii l narysuj linię równoległą do linii l. Punkt przecięcia tej linii z płaszczyzną p nazywamy rzutem równoległym punktu A do płaszczyzny p w kierunku prostej l. Oznaczmy to A". Jeśli punkt A należy do linii l, następnie rzut równoległy A do płaszczyzny p jest uważany za punkt przecięcia prostej l z samolotem str.

W ten sposób każdy punkt A przestrzeń jest odwzorowywana na jej projekcję A" na płaszczyznę p. Ta zgodność nazywana jest rzutem równoległym na płaszczyznę p w kierunku prostej l.

Grupa przekształceń rzutowych. Zastosowanie do rozwiązywania problemów.

Pojęcie rzutowej transformacji płaszczyzny. Przykłady przekształceń płaszczyzny rzutowej. Własności przekształceń rzutowych. Homologia, własności homologii. Grupa przekształceń rzutowych.

Pojęcie rzutowej transformacji płaszczyzny: Pojęcie transformacji rzutowej uogólnia pojęcie projekcji centralnej. Jeżeli wykonamy centralny rzut płaszczyzny α na jakąś płaszczyznę α 1 , to rzut α 1 na α 2 , α 2 na α 3 , ... i wreszcie na jakąś płaszczyznę α N znowu na α 1 , to złożenie wszystkich tych rzutów jest przekształceniem rzutowym płaszczyzny α; taki łańcuch może zawierać równoległe projekcje.

Przykłady przekształceń płaszczyzny rzutowej: Transformacja rzutowa płaszczyzny rozszerzonej to jej odwzorowanie jeden do jednego na samą siebie, które zachowuje współliniowość punktów, czyli innymi słowy obraz dowolnej linii prostej jest linią prostą. Każda transformacja rzutowa jest złożeniem łańcucha projekcji centralnych i równoległych. Transformacja afiniczna jest szczególnym przypadkiem transformacji rzutowej, w której prosta w nieskończoności wchodzi w siebie.

Własności przekształceń rzutowych:

W ramach transformacji rzutowej trzy punkty, które nie leżą na linii, są odwzorowywane na trzy punkty, które nie leżą na linii.

W ramach transformacji rzutowej rama przechodzi do ramki.

W przypadku przekształcenia rzutowego linia przechodzi w linię prostą, snop przechodzi w snop.

Homologia, właściwości homologii:

Transformacja rzutowa płaszczyzny, która ma linię niezmiennych punktów, a zatem ołówek niezmiennych linii, nazywana jest homologią.

1. Linia przechodząca przez odpowiednie, nie pokrywające się punkty homologii jest linią niezmienniczą;

2. Linie przechodzące przez odpowiednie nie pokrywające się punkty homologii należą do tego samego ołówka, którego środek jest niezmiennym punktem.

3. Punkt, jego obraz i środek homologii leżą na tej samej linii prostej.

Grupa przekształceń rzutowych: rozważ rzutowe odwzorowanie płaszczyzny rzutowej P 2 na samą siebie, czyli rzutowe przekształcenie tej płaszczyzny (P 2 ’ = P 2).

Tak jak poprzednio, złożenie f przekształceń rzutowych f 1 i f 2 płaszczyzny rzutowej P 2 jest wynikiem kolejnego wykonania przekształceń f 1 i f 2: f = f 2 °f 1 .

Twierdzenie 1: Zbiór H wszystkich przekształceń rzutowych płaszczyzny rzutowej P 2 jest grupą wchodzącą w skład przekształceń rzutowych.

Formy kwadratowe

forma kwadratowa f(x 1, x 2,..., x n) n zmiennych nazywamy sumą, której każdy wyraz jest albo kwadratem jednej ze zmiennych, albo iloczynem dwóch różnych zmiennych, wziętym z pewnym współczynnikiem: f(x 1, x 2, ..., x n) = (a ij = a ji).

Macierz A, złożona z tych współczynników, nazywana jest macierzą postaci kwadratowej. Zawsze symetryczny macierz (tj. macierz symetryczna względem głównej przekątnej, a ij = a ji).

W notacji macierzowej postać kwadratowa ma postać f(X) = X T AX, gdzie

Rzeczywiście

Na przykład napiszmy formę kwadratową w postaci macierzowej.

Aby to zrobić, znajdujemy macierz formy kwadratowej. Jego elementy diagonalne są równe współczynnikom przy kwadratach zmiennych, a pozostałe elementy są równe połowie odpowiednich współczynników postaci kwadratowej. Dlatego

Niech kolumna-macierz zmiennych X będzie otrzymana przez niezdegenerowaną transformację liniową kolumny-macierzy Y, tj. X = CY, gdzie C jest niezdegenerowaną macierzą rzędu n. Następnie forma kwadratowa
f(X) \u003d X T AX \u003d (CY) T A (CY) \u003d (Y T C T) A (CY) \u003d Y T (CT T AC) Y.

Zatem przy niezdegenerowanej transformacji liniowej C macierz postaci kwadratowej przyjmuje postać: A * = C T AC.

Na przykład znajdźmy postać kwadratową f(y 1, y 2) uzyskaną z postaci kwadratowej f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 przez transformację liniową.

Forma kwadratowa nazywa się kanoniczny(To ma pogląd kanoniczny) jeśli wszystkie jego współczynniki a ij = 0 dla i ≠ j, tj.
f(x 1, x 2,...,x n) = za 11 x 1 2 + za 22 x 2 2 + ... + za nn x n 2 = .

Jego macierz jest diagonalna.

Twierdzenie(dowód nie jest tutaj podany). Dowolną formę kwadratową można sprowadzić do postaci kanonicznej za pomocą niezdegenerowanej transformacji liniowej.

Na przykład sprowadźmy formę kwadratową do postaci kanonicznej
fa (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Aby to zrobić, najpierw wybierz pełny kwadrat dla zmiennej x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Teraz wybieramy pełny kwadrat dla zmiennej x 2:

fa (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 - 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) - (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 - (1/20) x 3 2.

Następnie niezdegenerowana transformacja liniowa y 1 \u003d x 1 + x 2, y 2 \u003d x 2 - (1/10) x 3 i y 3 \u003d x 3 doprowadza tę formę kwadratową do postaci kanonicznej f (y 1 , y 2, y 3) = 2 y 1 2 - 5 y 2 2 - (1/20) y 3 2 .

Należy zauważyć, że forma kanoniczna formy kwadratowej jest zdefiniowana niejednoznacznie (tę samą formę kwadratową można sprowadzić do formy kanonicznej na różne sposoby). Jednak formy kanoniczne uzyskiwane różnymi metodami mają szereg wspólnych właściwości. W szczególności liczba terminów o dodatnich (ujemnych) współczynnikach formy kwadratowej nie zależy od tego, jak forma jest zredukowana do tej postaci (na przykład w rozważanym przykładzie zawsze będą dwa współczynniki ujemne i jeden dodatni). Ta właściwość nazywa się prawo bezwładności form kwadratowych.

Sprawdźmy to, sprowadzając tę ​​samą formę kwadratową do postaci kanonicznej w inny sposób. Zacznijmy transformację od zmiennej x 2:
fa (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 -
- 2 * x 2 ((1/6) x 3 + (2/3) x 1) + ((1/6) x 3 + (2/3) x 1) 2) - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 - (1/6) x 3 - (2/3) x 1) 2 - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2, gdzie y 1 \u003d - (2/3) x 1 + x 2 - (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 i y 3 = x 1 . Tutaj dodatni współczynnik 2 dla y 3 i dwa ujemne współczynniki (-3) dla y 1 i y 2 (inną metodą otrzymaliśmy dodatni współczynnik 2 dla y 1 i dwa ujemne współczynniki - (-5) dla y 2 i (-1/20) dla y 3).

Należy również zauważyć, że rząd macierzy postaci kwadratowej, tzw ranga formy kwadratowej, jest równa liczbie niezerowych współczynników postaci kanonicznej i nie zmienia się przy przekształceniach liniowych.

Forma kwadratowa f(X) jest nazywana pozytywnie (negatywny) niektórzy, jeśli dla wszystkich wartości zmiennych, które nie są jednocześnie równe zeru, jest dodatnia, tj. f(X) > 0 (ujemne, tj.
f(X)< 0).

Na przykład forma kwadratowa f 1 (X) \u003d x 1 2 + x 2 2 jest dodatnio określona, ​​ponieważ jest sumą kwadratów, a forma kwadratowa fa 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 jest określona ujemnie, ponieważ reprezentuje to może być reprezentowane jako f 2 (X) \u003d - (x 1 - x 2) 2.

W większości praktycznych sytuacji nieco trudniej jest ustalić oznaczalność formy kwadratowej, dlatego stosuje się do tego jedno z następujących twierdzeń (formułujemy je bez dowodów).

Twierdzenie. Forma kwadratowa jest dodatnia (ujemna) określona wtedy i tylko wtedy, gdy wszystkie wartości własne jej macierzy są dodatnie (ujemne).

Twierdzenie (kryterium Sylwestra). Forma kwadratowa jest dodatnio określona wtedy i tylko wtedy, gdy wszystkie główne drugorzędne macierzy tej postaci są dodatnie.

Major (narożnik) minor K-ty rząd macierzy A n-tego rzędu nazywany jest wyznacznikiem macierzy złożonej z pierwszych k wierszy i kolumn macierzy A ().

Zauważ, że w przypadku form kwadratowych o ujemnie określonych znakach głównych drugorzędnych naprzemiennie, a drugorzędny pierwszego rzędu musi być ujemny.

Na przykład badamy postać kwadratową f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 pod kątem określoności znaku.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
. Dlatego forma kwadratowa jest dodatnio określona.

Metoda 2. Główny drugorzędny pierwszego rzędu macierzy A D 1 = a 11 = 2 > 0. Główny drugorzędny drugiego rzędu D 2 = = 6 - 4 = 2 > 0. Zatem zgodnie z kryterium Sylwestra forma kwadratowa jest dodatnio określona.

Badamy inną formę kwadratową dla określenia znaku, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metoda 1. Skonstruujmy macierz postaci kwadratowej A = . Równanie charakterystyczne będzie miało postać = (-2 - l)*
*(-3 - l) - 4 \u003d (6 + 2l + 3l + l 2) - 4 \u003d l 2 + 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
. Dlatego forma kwadratowa jest ujemnie określona.

Kwadratowe kształty.
Znaczenie form. Kryterium Sylwestra

Przymiotnik „kwadrat” od razu sugeruje, że coś tu jest związane z kwadratem (drugiego stopnia), a już wkrótce dowiemy się, co to „coś” i jaka jest forma. Wyszło od razu :)

Witam na mojej nowej lekcji, a jako natychmiastową rozgrzewkę przyjrzymy się kształtowi paska liniowy. Forma liniowa zmienne zwany jednorodny Wielomian I stopnia:

- kilka konkretnych liczb * (zakładamy, że przynajmniej jedna z nich jest różna od zera) i są zmiennymi, które mogą przyjmować dowolne wartości.

* W tym temacie rozważymy tylko liczby rzeczywiste .

Spotkaliśmy się już z terminem „jednorodny” w lekcji o jednorodne układy równań liniowych, aw tym przypadku oznacza to, że wielomian nie ma dodanej stałej.

Na przykład: – postać liniowa dwóch zmiennych

Teraz kształt jest kwadratowy. forma kwadratowa zmienne zwany jednorodny wielomian drugiego stopnia, każdy termin którego zawiera kwadrat zmiennej lub podwójnie iloczyn zmiennych. Na przykład postać kwadratowa dwóch zmiennych ma następującą postać:

Uwaga! To jest standardowy wpis i nie musisz nic w nim zmieniać! Pomimo „okropnego” wyglądu wszystko jest tutaj proste - podwójne indeksy stałych sygnalizują, które zmienne są zawarte w jednym lub drugim terminie:
– to określenie zawiera iloczyn i (kwadrat);
- oto praca;
- a oto praca.

- Od razu przewiduję rażący błąd, gdy gubią „minus” współczynnika, nie zdając sobie sprawy, że odnosi się on do terminu:

Czasami pojawia się „szkolna” wersja projektu w duchu, ale tylko czasami. Nawiasem mówiąc, zauważ, że stałe tutaj nic nam nie mówią, dlatego trudniej jest zapamiętać „łatwy zapis”. Zwłaszcza, gdy jest więcej zmiennych.

A forma kwadratowa trzech zmiennych zawiera już sześć wyrazów:

... dlaczego „dwa” mnożniki są umieszczane w terminach „mieszanych”? Jest to wygodne i wkrótce stanie się jasne, dlaczego.

Jednak zapiszemy ogólną formułę, wygodnie jest ułożyć ją za pomocą „arkusza”:

- uważnie przestudiuj każdą linijkę - nie ma w tym nic złego!

Forma kwadratowa zawiera wyrazy ze zmiennymi kwadratowymi i wyrazy z ich iloczynami w parach (cm. kombinatoryczna formuła kombinacji) . Nic więcej - bez „samotnego x” i bez dodanej stałej (wtedy nie otrzymujesz formy kwadratowej, ale heterogeniczny wielomian drugiego stopnia).

Notacja macierzowa formy kwadratowej

W zależności od wartości rozpatrywana postać może przyjmować zarówno wartości dodatnie, jak i ujemne, i to samo dotyczy dowolnej postaci liniowej – jeśli przynajmniej jeden z jej współczynników jest niezerowy, to może okazać się albo dodatnia, albo ujemna (w zależności od na wartościach).

Ta forma nazywa się zmienny. A jeśli wszystko jest przezroczyste w przypadku formy liniowej, to w przypadku formy kwadratowej jest znacznie ciekawiej:

Jest całkiem jasne, że ta forma może przyjmować wartości dowolnego znaku, a więc forma kwadratowa może być również naprzemienna.

Może nie być:

– zawsze, chyba że oba są równe zeru.

- dla kazdego wektor oprócz zera.

I ogólnie mówiąc, jeśli za jakiekolwiek niezerowe wektor , , to nazywamy formę kwadratową pozytywnie określony; Jeśli następnie ujemnie określony.

I wszystko byłoby dobrze, ale określoność formy kwadratowej jest widoczna tylko w prostych przykładach, a ta widoczność jest tracona już przy niewielkiej komplikacji:
– ?

Można przypuszczać, że forma jest pozytywnie zdefiniowana, ale czy tak jest w rzeczywistości? Nagle pojawiają się wartości, przy których jest mniejsze od zera?

Z tego powodu tam twierdzenie: Jeśli wszyscy wartości własne macierze postaci kwadratowej są dodatnie * , to jest zdefiniowany dodatnio. Jeśli wszystkie są ujemne, to jest ujemne.

* Teoretycznie udowodniono, że wszystkie wartości własne rzeczywistej macierzy symetrycznej ważny

Napiszmy macierz powyższej postaci:
i z równania znajdźmy ją wartości własne:

Rozwiązujemy stare dobre równanie kwadratowe:

, więc forma jest pozytywnie zdefiniowany, tj. dla dowolnych wartości niezerowych jest większa od zera.

Rozważana metoda wydaje się działać, ale jest jedno duże ALE. Już dla macierzy trzy na trzy szukanie wartości własnych jest długim i nieprzyjemnym zadaniem; z dużym prawdopodobieństwem otrzymasz wielomian 3 stopnia z niewymiernymi pierwiastkami.

Jak być? Jest łatwiejszy sposób!

Kryterium Sylwestra

Nie, nie Sylvester Stallone :) Na początek przypomnę co drobne kątowe macierze. Ten wyznaczniki które "wyrastają" z jego lewego górnego rogu:

a ostatni jest dokładnie równy wyznacznikowi macierzy.

Teraz faktycznie kryterium:

1) Zdefiniowana forma kwadratowa pozytywnie wtedy i tylko wtedy, gdy WSZYSTKIE jego mniejsze kątowe są większe od zera: .

2) Zdefiniowana forma kwadratowa negatywny wtedy i tylko wtedy, gdy jego mniejsze kątowe zmieniają się w znaku, podczas gdy pierwsza mniejsza jest mniejsza od zera: , , jeśli jest parzysta lub , jeśli jest nieparzysta.

Jeśli co najmniej jeden kątowy mniejszy ma przeciwny znak, to forma naprzemienny znak. Jeśli mniejsze kątowe są tego znaku, ale są wśród nich zera, to jest to szczególny przypadek, który przeanalizuję nieco później, po kliknięciu na bardziej powszechne przykłady.

Przeanalizujmy kątowe drugorzędne macierzy :

A to od razu mówi nam, że forma nie jest zdeterminowana negatywnie.

Wniosek: wszystkie mniejsze kąty są większe od zera, więc kształt pozytywnie zdefiniowany.

Czy istnieje różnica w stosunku do metody wartości własnej? ;)

Piszemy macierz kształtu z Przykład 1:

jego pierwszy mniejszy kątowy i drugi , stąd wynika, że ​​forma jest naprzemienna, tj. w zależności od wartości , może przyjmować zarówno wartości dodatnie, jak i ujemne. Jednak to jest takie oczywiste.

Weź formę i jej macierz z Przykład 2:

tutaj w ogóle bez wglądu nie do zrozumienia. Ale z kryterium Sylwestra nie obchodzi nas:
, stąd forma na pewno nie jest ujemna.

i na pewno nie pozytywne. (ponieważ wszystkie podrzędne kąty muszą być dodatnie).

Wniosek: kształt jest naprzemienny.

Przykłady rozgrzewki do samodzielnego rozwiązania:

Przykład 4

Zbadaj formy kwadratowe pod kątem określoności znaku

A)

W tych przykładach wszystko jest płynne (patrz koniec lekcji), ale w rzeczywistości, aby wykonać takie zadanie Kryterium Sylwestra może nie być wystarczające.

Rzecz w tym, że istnieją przypadki „graniczne”, a mianowicie: jeśli dla każdego niezerowe vector , to kształt jest zdefiniowany nieujemne, Jeśli następnie niepozytywne. Te formy mają niezerowe wektory, dla których .

Tutaj możesz przynieść taki „akordeon guzikowy”:

Podświetlanie pełny kwadrat, od razu widzimy nienegatywność postać: , ponadto jest równa zeru dla dowolnego wektora o równych współrzędnych, na przykład: .

Przykład „lustra”. niepozytywne pewna forma:

i jeszcze bardziej trywialny przykład:
– tutaj postać jest równa zeru dla dowolnego wektora , gdzie jest dowolną liczbą.

Jak ujawnić nienegatywność lub niepozytywność formy?

Do tego potrzebujemy koncepcji główne nieletnie macierze. Moll główny to minor złożony z elementów znajdujących się na przecięciu rzędów i kolumn o tych samych numerach. Tak więc macierz ma dwa główne drugorzędne pierwszego rzędu:
(element znajduje się na przecięciu 1. rzędu i 1. kolumny);
(element znajduje się na przecięciu drugiego rzędu i drugiej kolumny),

i jeden główny drugorzędny drugiego rzędu:
- złożony z elementów 1., 2. rzędu oraz 1., 2. kolumny.

Matryca „trzy na trzy” Jest siedem głównych nieletnich, a tutaj już musisz machać bicepsem:
- troje nieletnich I stopnia,
troje nieletnich II rzędu:
- złożony z elementów 1., 2. rzędu i 1., 2. kolumny;
- złożony z elementów 1., 3. rzędu i 1., 3. kolumny;
- złożony z elementów 2, 3 rzędu i 2, 3 kolumny,
i jeden mniejszy III rzędu:
- złożony z elementów 1., 2., 3. rzędu oraz 1., 2. i 3. kolumny.
Ćwiczenia dla zrozumienia: zapisz wszystkie główne drugorzędne matrycy .
Sprawdzamy na końcu lekcji i kontynuujemy.

Kryterium Schwarzeneggera:

1) Zdefiniowano niezerową* postać kwadratową nieujemne wtedy i tylko wtedy, gdy WSZYSTKIE jego główne nieletnie nieujemne(większe lub równe zeru).

* Zerowa (zdegenerowana) postać kwadratowa ma wszystkie współczynniki równe zeru.

2) Niezerowa forma kwadratowa ze zdefiniowaną macierzą niepozytywne wtedy i tylko wtedy, gdy jest to:
– główni małoletni I stopnia niepozytywne(mniejszy lub równy zeru);
są głównymi nieletnimi II stopnia nieujemne;
– główni małoletni III rzędu niepozytywne(rozpoczęła się zmiana);
…
– dur moll rzędu niepozytywne, jeśli jest nieparzyste lub nieujemne, jeśli jest parzysta.

Jeśli co najmniej jeden nieletni ma przeciwny znak, wówczas forma jest naprzemienna.

Zobaczmy, jak działa kryterium w powyższych przykładach:

Zróbmy macierz kształtów i Po pierwsze obliczmy mniejsze kątowe - co jeśli jest zdefiniowane dodatnio lub ujemnie?

Uzyskane wartości nie spełniają jednak kryterium sylwestrowego drugiego nieletniego nie negatywny, co powoduje konieczność sprawdzenia drugiego kryterium (w przypadku drugiego kryterium nie zostanie ono spełnione automatycznie, tj. od razu wyciągnie się wniosek o przemianie znaku formy).

Wielcy nieletni pierwszego rzędu:
- są pozytywne
II stopnia dur moll:
- nie negatywny.

Zatem WSZYSTKIE drugorzędne durowe są nieujemne, więc forma nieujemne.

Napiszmy macierz postaci , dla którego oczywiście kryterium Sylwestra nie jest spełnione. Ale nie otrzymaliśmy również przeciwnych znaków (bo oba mniejsze kątowe są równe zeru). W związku z tym sprawdzamy spełnienie kryterium nienegatywności/niepozytywności. Wielcy nieletni pierwszego rzędu:
- nie pozytywne
II stopnia dur moll:
- nie negatywny.

Zatem zgodnie z kryterium Schwarzeneggera (pkt 2) forma jest określona niepozytywnie.

Teraz, w pełni uzbrojeni, przeanalizujemy bardziej zabawny problem:

Przykład 5

Zbadaj formę kwadratową pod kątem określoności znaku

Ta forma jest ozdobiona porządkiem „alfa”, który może być równy dowolnej liczbie rzeczywistej. Ale będzie tylko zabawniej decydować.

Najpierw zapiszmy matrycę formularza, prawdopodobnie wielu już przystosowało się do tego ustnie: główna przekątna w kwadratach umieszczamy współczynniki, aw miejscach symetrycznych - półwspółczynniki odpowiednich produktów „mieszanych”:

Obliczmy mniejsze kąty:

Rozszerzę trzeci wyznacznik wzdłuż trzeciej linii:

W tej sekcji skupimy się na specjalnej, ale ważnej klasie dodatnich form kwadratowych.

Definicja 3. Prawdziwa forma kwadratowa nazywana jest nieujemną (niepozytywną), jeśli dla dowolnych rzeczywistych wartości zmiennych

. (35)

W tym przypadku symetryczna macierz współczynników nazywana jest dodatnią półokreśloną (ujemną półokreśloną).

Definicja 4. Prawdziwa forma kwadratowa nazywana jest dodatnio-określoną (określoną ujemnie), jeśli dla dowolnych rzeczywistych wartości zmiennych, które nie są jednocześnie równe zeru

. (36)

W tym przypadku macierz jest również nazywana dodatnio określoną (ujemnie określoną).

Klasa form dodatnio-określonych (negatywno-określonych) należy do klasy form nienegatywnych (odpowiednio niepozytywnych).

Niech będzie dana forma nie przecząca. Przedstawiamy to jako sumę niezależnych kwadratów:

. (37)

W tej reprezentacji wszystkie kwadraty muszą być dodatnie:

. (38)

Rzeczywiście, gdyby były jakieś , to można by wybrać takie wartości, dla których

Ale wtedy dla tych wartości zmiennych forma miałaby wartość ujemną, co jest niemożliwe ze względu na warunek. Oczywiście odwrotnie, z (37) i (38) wynika, że ​​forma jest dodatnia.

Zatem nieujemna forma kwadratowa charakteryzuje się równościami .

Niech teraz będzie dodatnio określoną formą. Następnie także forma nieujemna. Dlatego można go przedstawić w postaci (37), gdzie wszystkie są dodatnie. Z pozytywnej określoności formy wynika, że ​​. Rzeczywiście, w przypadku można wybrać takie wartości, które nie są jednocześnie równe zeru, dla których wszystkie zniknęłyby. Ale wtedy, na mocy (37), w , co jest sprzeczne z warunkiem (36).

Łatwo zauważyć, że odwrotnie, jeśli w (37) i wszystkie są dodatnie, to jest dodatnio określona forma.

Innymi słowy, forma nieujemna jest dodatnio określona wtedy i tylko wtedy, gdy nie jest pojedyncza.

Następujące twierdzenie podaje kryterium pozytywnej określoności formy w postaci nierówności, które muszą być spełnione przez współczynniki formy. W tym przypadku stosuje się notację napotkaną już w poprzednich rozdziałach dla kolejnych głównych drugorzędnych macierzy:

.

Twierdzenie 3. Aby forma kwadratowa była dodatnio określona, ​​konieczne i wystarczające jest, aby nierówności

Dowód. Wystarczalność warunków (39) wynika bezpośrednio ze wzoru Jacobiego (28). Konieczność warunków (39) ustala się w następujący sposób. Z pozytywnej określoności formy wynika pozytywna określoność form „skróconych”.

.

Ale wtedy wszystkie te formy muszą być inne niż w liczbie pojedynczej, tj.

Teraz mamy możliwość skorzystania ze wzoru Jacobiego (28) (dla ). Ponieważ po prawej stronie tego wzoru wszystkie kwadraty muszą być dodatnie, więc

To pociąga za sobą nierówności (39). Twierdzenie zostało udowodnione.

Ponieważ dowolny główny drugorzędny macierzy, przy odpowiednim przenumerowaniu zmiennych, można umieścić w lewym górnym rogu, mamy

Konsekwencja. W dodatnio określonej postaci kwadratowej wszystkie główne drugorzędne macierzy współczynników są dodatnie:

Komentarz. Od nienegatywności kolejnych głównych nieletnich

nie wynika z nienegatywności formy. Rzeczywiście, forma

,

w której , spełnia warunki , ale nie jest nieujemna.

Jest jednak co następuje

Twierdzenie 4. Aby forma kwadratowa była nieujemna, konieczne i wystarczające jest, aby wszystkie mniejsze główne jej macierzy współczynników były nieujemne:

Dowód. Wprowadźmy formę pomocniczą, która nie jest dodatnia, jest konieczna i wystarczająca dla nierówności

Facebook

Świergot

W kontakcie z

Koledzy z klasy

Google Plus