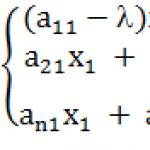The matrix notation of the quadratic form has the form. Positive definite quadratic forms
Positive definite quadratic forms
Definition. Quadratic form from n unknown is called positive definite, if its rank is equal to the positive index of inertia and is equal to the number of unknowns.
Theorem. A quadratic form is positive definite if and only if it takes positive values on any nonzero set of variable values.
Proof. Let the quadratic form be a non-degenerate linear transformation of the unknowns
returned to normal
.
For any non-zero set of variable values, at least one of the numbers 
different from zero, i.e. . The necessity of the theorem is proved.
Assume that the quadratic form takes positive values on any non-zero set of variables, but its index of inertia is positive. By a non-degenerate linear transformation of the unknowns
Let's bring it back to normal. Without loss of generality, we can assume that in this normal form the square of the last variable is either absent or enters it with a minus sign, i.e. 
, where or . Suppose that is a non-zero set of values of variables , obtained as a result of solving the system of linear equations
In this system, the number of equations is equal to the number of variables and the determinant of the system is nonzero. By Cramer's theorem, the system has a unique solution, and it is nonzero. For this set. Contradiction with the condition. We arrive at a contradiction with the assumption, which proves the sufficiency of the theorem.
Using this criterion, it is not possible to determine from the coefficients whether a quadratic form is positive-definite. The answer to this question is given by another theorem, for the formulation of which we introduce one more concept. Principal Diagonal Matrix Minors are the minors located in its upper left corner:
,
, 
, … , 
.
Theorem.A quadratic form is positive definite if and only if all its principal diagonal minors are positive.
Proof we will carry out by the method of complete mathematical induction on the number n quadratic form variables f.
Hypothesis of induction. Assume that for quadratic forms with fewer variables n the statement is correct.
Consider the quadratic form from n variables. Collect in one bracket all the terms containing . The remaining terms form a quadratic form in variables. By the induction hypothesis, the statement is true for it.
Assume that the quadratic form is positive definite. Then the quadratic form is also positive definite. If we assume that this is not the case, then there is a non-zero set of variable values 
, for which 
and correspondingly, 
, which contradicts the fact that the quadratic form is positive definite. By the induction hypothesis, all principal diagonal minors of a quadratic form are positive, i.e. all first principal minors of a quadratic form f are positive. Last principal minor of a quadratic form –
is the determinant of its matrix. This determinant is positive, since its sign coincides with the sign of the matrix of its normal form, i.e. with the sign of the identity matrix determinant.
Let all principal diagonal minors of the quadratic form be positive. Then all principal diagonal minors of the quadratic form are positive from the equality 
. By the induction hypothesis, the quadratic form is positive definite, so there is a non-degenerate linear transformation of variables that reduces the form to the form of the sum of squares of new variables . This linear transformation can be extended to a nondegenerate linear transformation of all variables by setting . The quadratic form is reduced by this transformation to the form
The concept of a quadratic form. Matrix of quadratic form. Canonical form of a quadratic form. Lagrange method. The normal form of a quadratic form. Rank, index and signature of a quadratic form. Positive definite quadratic form. Quadrics.
The concept of a quadratic form: a function on a vector space given by a homogeneous polynomial of the second degree in the coordinates of the vector.
quadratic form from n unknown 
is called the sum, each term of which is either the square of one of these unknowns, or the product of two different unknowns.
Quadratic Matrix: The matrix is called the matrix of quadratic form in the given basis. If the field characteristic is not equal to 2, we can assume that the matrix of the quadratic form is symmetric, that is, .
Write a matrix of quadratic form:
Hence,
In vector-matrix form, the quadratic form is:
A , where 
Canonical form of a quadratic form: A quadratic form is called canonical if all 
i.e.
Any quadratic form can be reduced to a canonical form using linear transformations. In practice, the following methods are usually used.
Lagrange method : successive selection of full squares. For example, if
Then a similar procedure is done with the quadratic form 
etc. If in quadratic form everything but is 
then, after a preliminary transformation, the matter is reduced to the procedure considered. Thus, if, for example, then we set 
The normal form of a quadratic form is: A normal quadratic form is a canonical quadratic form in which all coefficients are equal to +1 or -1.
Rank, index and signature of a quadratic form: The rank of the quadratic form A called the rank of the matrix A. The rank of a quadratic form does not change under nondegenerate transformations of the unknowns.
The number of negative coefficients is called the negative shape index.
The number of positive terms in the canonical form is called the positive index of inertia of the quadratic form, the number of negative terms is called the negative index. The difference between positive and negative indices is called the signature of the quadratic form
Positive definite quadratic form: Real quadratic form 
is called positive-definite (negative-definite) if for any real values of the variables that are not simultaneously equal to zero
. (36)
In this case, the matrix is also called positive definite (negative definite).
The class of positive-definite (negative-definite) forms is part of the class of non-negative (respectively, non-positive) forms.
Quads: Quadric - n-dimensional hypersurface in n+1-dimensional space, defined as the set of zeros of a polynomial of the second degree. If you enter the coordinates ( x 1 , x 2 , x n+1 ) (in Euclidean or affine space), the general quadric equation has the form
This equation can be rewritten more compactly in matrix notation:
where x = ( x 1 , x 2 , x n+1 ) is a row vector, x T is the transposed vector, Q is the size matrix ( n+1)×( n+1) (it is assumed that at least one of its elements is nonzero), P is a row vector, and R is a constant. Most often, quadrics are considered over real or complex numbers. The definition can be extended to quadrics in projective space, see below.
More generally, the set of zeros of a system of polynomial equations is known as an algebraic variety. Thus a quadric is an (affine or projective) algebraic variety of second degree and codimension 1.
Plane and space transformations.
Plane transformation definition. Definition of movement. motion properties. Two types of movements: movement of the first kind and movement of the second kind. Movement examples. Analytical expression of motion. Classification of plane motions (depending on the presence of fixed points and invariant lines). Group of plane motions.
Plane transformation definition: Definition. A plane transformation that preserves the distance between points is called movement(or displacement) of the plane. The plane transformation is called affine, if it takes any three points lying on the same line to three points also lying on the same line and at the same time preserves the simple relation of the three points.
Movement definition: This is a shape transformation that preserves the distances between points. If two figures are exactly combined with each other by means of movement, then these figures are the same, equal.
Movement properties: every orientation-preserving motion of a plane is either a parallel translation or a rotation; every orientation-changing motion of a plane is either an axial symmetry or a sliding symmetry. Points lying on a straight line, when moving, pass into points lying on a straight line, and the order of their mutual arrangement is preserved. When moving, the angles between the half-lines are preserved.
Two types of movements: movement of the first kind and movement of the second kind: Movements of the first kind are those movements that preserve the orientation of the bases of a certain figure. They can be realized with continuous movements.
Movements of the second kind are those movements that change the orientation of the bases to the opposite. They cannot be realized by continuous movements.
Examples of movements of the first kind are translation and rotation around a straight line, and movements of the second kind are central and mirror symmetries.
The composition of any number of motions of the first kind is a motion of the first kind.
The composition of an even number of movements of the second kind is a movement of the 1st kind, and the composition of an odd number of movements of the 2nd kind is a movement of the 2nd kind.
Movement examples:Parallel transfer. Let a be a given vector. Parallel transfer to the vector a is the mapping of the plane onto itself, in which each point M is mapped to the point M 1, that the vector MM 1 is equal to the vector a.
Parallel translation is a movement because it is a mapping of the plane onto itself, preserving distances. Visually, this movement can be represented as a shift of the entire plane in the direction of a given vector a by its length.
Turn . Let us designate a point O on the plane ( turning center) and set the angle α ( angle of rotation). The rotation of the plane around the point O by the angle α is the mapping of the plane onto itself, in which each point M is mapped to the point M 1, that OM = OM 1 and the angle MOM 1 is equal to α. In this case, the point O remains in its place, i.e., it is displayed in itself, and all other points rotate around the point O in the same direction - clockwise or counterclockwise (the figure shows a counterclockwise rotation).
A turn is a movement because it is a mapping of the plane onto itself, which preserves distances.
Analytical expression of movement: the analytical connection between the coordinates of the pre-image and the image of the point has the form (1).
Classification of plane motions (depending on the presence of fixed points and invariant lines): Definition:
A point in a plane is invariant (fixed) if, under a given transformation, it transforms into itself.
Example: With central symmetry, the point of the center of symmetry is invariant. When turning, the point of the center of rotation is invariant. With axial symmetry, the line is invariant - the axis of symmetry is the line of invariant points.
Theorem: If the motion has no invariant point, then it has at least one invariant direction.
Example: Parallel transfer. Indeed, lines parallel to this direction are invariant as a figure as a whole, although it does not consist of invariant points.
Theorem: If some ray moves, the ray translates into itself, then this motion is either an identical transformation, or a symmetry with respect to the line containing the given ray.
Therefore, according to the presence of invariant points or figures, it is possible to classify movements.
| Movement name | Invariant points | Invariant lines |
| Movement of the first kind. | ||
| 1. - turn | (center) - 0 | No |
| 2. Identity transformation | all points of the plane | all straight |
| 3. Central symmetry | point 0 - center | all lines passing through point 0 |
| 4. Parallel transfer | No | all straight |
| Movement of the second kind. | ||
| 5. Axial symmetry. | set of points | axis of symmetry (straight) all straight |
Plane movement group: In geometry, self-coincidence groups of figures play an important role. If - some figure on the plane (or in space), then we can consider the set of all those movements of the plane (or space), in which the figure passes into itself.
This set is a group. For example, for an equilateral triangle, the group of plane motions that take the triangle into itself consists of 6 elements: rotations by angles around a point and symmetries about three lines.
They are shown in fig. 1 with red lines. The elements of the self-coincidence group of a regular triangle can be specified in another way. To clarify this, let's number the vertices of a regular triangle with numbers 1, 2, 3. can be conditionally entered in the form of one of these brackets:
etc.
where the numbers 1, 2, 3 denote the numbers of those vertices into which vertices 1, 2, 3 pass as a result of the considered movement.
Projective spaces and their models.
Concept of projective space and model of projective space. Basic facts of projective geometry. A bunch of lines centered at point O is a projective plane model. projective points. The extended plane is a model of the projective plane. An extended three-dimensional affine or Euclidean space is a projective space model. Images of plane and spatial figures in parallel design.
Concept of projective space and model of projective space:
A projective space over a field is a space consisting of lines (one-dimensional subspaces) of some linear space over a given field. The straight spaces are called dots projective space. This definition lends itself to generalization to an arbitrary body
If it has dimension , then the dimension of the projective space is called the number , and the projective space itself is denoted and is called associated with (to indicate this, the notation is adopted).
The transition from a vector space of dimension to the corresponding projective space is called projectivization spaces.
Points can be described using homogeneous coordinates.
Basic facts of projective geometry: Projective geometry is a branch of geometry that studies projective planes and spaces. The main feature of projective geometry is the principle of duality, which adds a graceful symmetry to many designs. Projective geometry can be studied both from a purely geometric point of view, and from an analytic (using homogeneous coordinates) and salgebraic point of view, considering the projective plane as a structure over a field. Often, and historically, the real projective plane is treated as the Euclidean plane with the addition of a "line at infinity".
Whereas the properties of the figures that Euclidean geometry deals with are metric(specific values of angles, segments, areas), and the equivalence of figures is equivalent to their congruence(i.e., when figures can be translated into one another by means of movement while preserving metric properties), there are more "deeper" properties of geometric figures that are preserved by transformations of a more general type than movement. Projective geometry studies the properties of figures that are invariant under the class projective transformations, as well as these transformations themselves.
Projective geometry complements Euclidean by providing beautiful and simple solutions to many problems complicated by the presence of parallel lines. The projective theory of conic sections is especially simple and elegant.
There are three main approaches to projective geometry: independent axiomatization, addition to Euclidean geometry, and structure over a field.
Axiomatization
A projective space can be defined using a different set of axioms.
Coxeter provides the following:
1. There is a line and a point is not on it.
2. There are at least three points on every line.
3. Exactly one straight line can be drawn through two points.
4. If A, B, C, And D different points and AB And CD intersect, then AC And BD intersect.
5. If ABC is a plane, then there is at least one point not in the plane ABC.
6. Two distinct planes intersect in at least two points.
7. Three diagonal points of a complete quadrilateral are not collinear.
8. If there are three points on a straight line X X
The projective plane (without the third dimension) is defined by somewhat different axioms:
1. Exactly one straight line can be drawn through two points.
2. Any two lines intersect.
3. There are four points, of which there are no three collinear.
4. Three diagonal points of complete quadrilaterals are not collinear.
5. If there are three points on a straight line X are invariant under the projectivity of φ, then all points on X are invariant with respect to φ.
6. Desargues' theorem: If two triangles are perspective through a point, then they are perspective through a line.
In the presence of a third dimension, Desargues' theorem can be proved without introducing the ideal point and line.
Extended plane - projective plane model: in an affine space A3, take a bundle of lines S(O) centered at a point O and a plane Π not passing through the center of the bundle: O 6∈ Π. A bundle of lines in an affine space is a model of the projective plane. Let's set the mapping of the set of points of the plane Π to the set of lines of the bundle S (Damn, pray if you got this question, I'm sorry)
Extended three-dimensional affine or Euclidean space - projective space model:
In order to make the mapping surjective, we repeat the process of formally extending the affine plane Π to the projective plane, Π, complementing the plane Π with a set of improper points (M∞) such that: ((M∞)) = P0(O). Since in the mapping the inverse image of each plane of the bundle of planes S(O) is a line on the plane d, it is obvious that the set of all improper points of the extended plane: Π = Π ∩ (M∞), (M∞), is an improper line d∞ of the extended plane which is the inverse image of the singular plane Π0: (d∞) = P0(O) (= Π0). (I.23) Let us agree that here and below we will understand the last equality P0(O) = Π0 in the sense of equality of sets of points, but endowed with different structures. Complementing the affine plane with an improper line, we have ensured that the mapping (I.21) becomes bijective on the set of all points of the extended plane:
Images of flat and spatial figures in parallel design:
In stereometry, spatial figures are studied, but in the drawing they are depicted as flat figures. How, then, should a spatial figure be depicted on a plane? Usually in geometry, parallel design is used for this. Let p be some plane, l- a straight line intersecting it (Fig. 1). Through an arbitrary point A, not belonging to the line l draw a line parallel to the line l. The point of intersection of this line with the plane p is called the parallel projection of the point A to the plane p in the direction of the straight line l. Let's denote it A". If the point A belongs to the line l, then the parallel projection A to the plane p is considered the point of intersection of the line l with plane p.
Thus, every point A space is mapped to its projection A" onto the plane p. This correspondence is called the parallel projection onto the plane p in the direction of the straight line l.
Group of projective transformations. Application to problem solving.
The concept of projective transformation of the plane. Examples of projective plane transformations. Properties of projective transformations. Homology, properties of homology. Group of projective transformations.
The concept of a projective plane transformation: The notion of a projective transformation generalizes the notion of a central projection. If we perform the central projection of the plane α onto some plane α 1 , then the projection of α 1 onto α 2 , α 2 onto α 3 , ... and, finally, some plane α n again on α 1 , then the composition of all these projections is the projective transformation of the plane α; such a chain can include parallel projections.
Examples of projective plane transformations: A projective transformation of an augmented plane is its one-to-one mapping onto itself, which preserves the collinearity of points, or, in other words, the image of any straight line is a straight line. Any projective transformation is a composition of a chain of central and parallel projections. An affine transformation is a special case of a projective one, in which the line at infinity goes into itself.
Properties of projective transformations:
Under a projective transformation, three points not on a line are mapped to three points not on a line.
Under a projective transformation, the frame goes over to the frame.
Under a projective transformation, a line goes into a straight line, a sheaf goes into a sheaf.
Homology, homology properties:
A projective transformation of a plane that has a line of invariant points and hence a pencil of invariant lines is called a homology.
1. A line passing through corresponding noncoinciding homology points is an invariant line;
2. The lines passing through the corresponding noncoinciding homology points belong to the same pencil, the center of which is an invariant point.
3. A point, its image, and the center of homology lie on the same straight line.
Group of projective transformations: consider a projective mapping of the projective plane P 2 onto itself, that is, a projective transformation of this plane (P 2 ’ = P 2).
As before, the composition f of projective transformations f 1 and f 2 of the projective plane P 2 is the result of successive execution of transformations f 1 and f 2: f = f 2 °f 1 .
Theorem 1: The set H of all projective transformations of the projective plane P 2 is a group under the composition of projective transformations.
Quadratic forms
quadratic form f(x 1, x 2,..., x n) of n variables is called the sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f(x 1, x 2, ...,x n) = (a ij = a ji).
The matrix A, composed of these coefficients, is called the quadratic form matrix. It's always symmetrical matrix (i.e., a matrix symmetric about the main diagonal, a ij = a ji).
In matrix notation, the quadratic form has the form f(X) = X T AX, where
Indeed
For example, let's write the quadratic form in matrix form.
To do this, we find a matrix of a quadratic form. Its diagonal elements are equal to the coefficients at the squares of the variables, and the remaining elements are equal to half of the corresponding coefficients of the quadratic form. That's why
Let the matrix-column of variables X be obtained by a non-degenerate linear transformation of the matrix-column Y, i.e. X = CY, where C is a non-degenerate matrix of order n. Then the quadratic form
f(X) \u003d X T AX \u003d (CY) T A (CY) \u003d (Y T C T) A (CY) \u003d Y T (C T AC) Y.
Thus, under a non-degenerate linear transformation C, the matrix of the quadratic form takes the form: A * = C T AC.
For example, let's find the quadratic form f(y 1, y 2) obtained from the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 by a linear transformation.
The quadratic form is called canonical(It has canonical view) if all its coefficients a ij = 0 for i ≠ j, i.e.
f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + ... + a nn x n 2 = .
Its matrix is diagonal.
Theorem(the proof is not given here). Any quadratic form can be reduced to a canonical form using a non-degenerate linear transformation.
For example, let us reduce to the canonical form the quadratic form
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
To do this, first select the full square for the variable x 1:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.
Now we select the full square for the variable x 2:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 - 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) - (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 - (1/20) x 3 2.
Then a non-degenerate linear transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 - (1/10) x 3 and y 3 \u003d x 3 brings this quadratic form to the canonical form f (y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .
Note that the canonical form of a quadratic form is defined ambiguously (the same quadratic form can be reduced to the canonical form in different ways). However, canonical forms obtained by various methods have a number of common properties. In particular, the number of terms with positive (negative) coefficients of a quadratic form does not depend on how the form is reduced to this form (for example, in the considered example there will always be two negative and one positive coefficient). This property is called the law of inertia of quadratic forms.
Let us verify this by reducing the same quadratic form to the canonical form in a different way. Let's start the transformation with the variable x 2:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 -
- 2 * x 2 ((1/6) x 3 + (2/3) x 1) + ((1/6) x 3 + (2/3) x 1) 2) - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 - (1/6) x 3 - (2/3) x 1) 2 - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2, where y 1 \u003d - (2/3) x 1 + x 2 - (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 and y 3 = x 1 . Here, a positive coefficient 2 for y 3 and two negative coefficients (-3) for y 1 and y 2 (and using another method, we got a positive coefficient 2 for y 1 and two negative coefficients - (-5) for y 2 and (-1 /20) for y 3).
It should also be noted that the rank of a matrix of a quadratic form, called the rank of the quadratic form, is equal to the number of non-zero coefficients of the canonical form and does not change under linear transformations.
The quadratic form f(X) is called positively (negative) certain, if for all values of the variables that are not simultaneously equal to zero, it is positive, i.e. f(X) > 0 (negative, i.e.
f(X)< 0).
For example, the quadratic form f 1 (X) \u003d x 1 2 + x 2 2 is positive definite, because is the sum of squares, and the quadratic form f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, because represents it can be represented as f 2 (X) \u003d - (x 1 - x 2) 2.
In most practical situations, it is somewhat more difficult to establish the sign-definiteness of a quadratic form, so one of the following theorems is used for this (we formulate them without proofs).
Theorem. A quadratic form is positive (negative) definite if and only if all eigenvalues of its matrix are positive (negative).
Theorem (Sylvester's criterion). A quadratic form is positive definite if and only if all principal minors of the matrix of this form are positive.
Major (corner) minor The k-th order of the matrix A of the n-th order is called the determinant of the matrix, composed of the first k rows and columns of the matrix A ().
Note that for negative-definite quadratic forms, the signs of the principal minors alternate, and the first-order minor must be negative.
For example, we examine the quadratic form f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign-definiteness.
= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17; 
. Therefore, the quadratic form is positive definite.
Method 2. The main minor of the first order of the matrix A D 1 = a 11 = 2 > 0. The main minor of the second order D 2 = = 6 - 4 = 2 > 0. Therefore, according to the Sylvester criterion, the quadratic form is positive definite.
We examine another quadratic form for sign-definiteness, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Method 1. Let's construct a matrix of quadratic form А = . The characteristic equation will have the form 
= (-2 - l)*
*(-3 - l) - 4 \u003d (6 + 2l + 3l + l 2) - 4 \u003d l 2 + 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17; 
. Therefore, the quadratic form is negative definite.
Square shapes.
Significance of forms. Sylvester's criterion
The adjective "square" immediately suggests that something here is connected with a square (second degree), and very soon we will know this "something" and what a form is. Turned out straight away :)
Welcome to my new lesson, and as an immediate warm-up, we will look at the striped shape linear. Linear form variables called homogeneous 1st degree polynomial:
- some specific numbers *
(we assume that at least one of them is different from zero), and are variables that can take arbitrary values.
* In this topic, we will only consider real numbers .
We have already encountered the term "homogeneous" in the lesson about homogeneous systems of linear equations, and in this case it implies that the polynomial does not have an added constant .
For example: 
– linear form of two variables
Now the shape is quadratic. quadratic form variables called homogeneous 2nd degree polynomial, each term of which contains either the square of the variable or double product of variables. So, for example, the quadratic form of two variables has the following form:
Attention! This is a standard entry, and you do not need to change anything in it! Despite the “terrible” look, everything is simple here - double subscripts of constants signal which variables are included in one or another term:
– this term contains the product and (square);
- here is the work;
- and here is the work.
- I immediately anticipate a gross mistake when they lose the "minus" of the coefficient, not realizing that it refers to the term:
Sometimes there is a "school" version of the design in the spirit, but then only sometimes. By the way, note that the constants here do not tell us anything at all, and therefore it is more difficult to remember the “easy notation”. Especially when there are more variables.
And the quadratic form of three variables already contains six terms:
... why are "two" multipliers put in the "mixed" terms? This is convenient, and it will soon become clear why.
However, we will write down the general formula, it is convenient to arrange it with a “sheet”:
- carefully study each line - there's nothing wrong with that!
The quadratic form contains terms with squared variables and terms with their pair products (cm. combinatorial formula of combinations) . Nothing else - no "lonely x" and no added constant (then you get not a quadratic form, but heterogeneous 2nd degree polynomial).
Matrix notation of a quadratic form
Depending on the values, the considered form can take both positive and negative values, and the same applies to any linear form - if at least one of its coefficients is non-zero, then it can turn out to be either positive or negative (depending on values).
This form is called alternating. And if everything is transparent with the linear form, then things are much more interesting with the quadratic form:
It is quite clear that this form can take on the values of any sign, thus, the quadratic form can also be alternating.
It may not be:
– always, unless both are equal to zero.
- for anyone vector except for zero.
And generally speaking, if for any non-zero vector , , then the quadratic form is called positive definite; if - then negative definite.
And everything would be fine, but the definiteness of the quadratic form is visible only in simple examples, and this visibility is lost already with a slight complication: 
– ?
One might assume that the form is positively defined, but is it really so? Suddenly there are values at which it is less than zero?
On this account, there theorem: If everyone eigenvalues matrices of quadratic form are positive * , then it is positively defined. If all are negative, then it is negative.
* It is proved in theory that all eigenvalues of a real symmetric matrix valid
Let's write the matrix of the above form: 
and from the equation 
let's find her eigenvalues:
We solve the good old quadratic equation:
, so the form 
is positively defined, i.e. for any non-zero values, it is greater than zero.
The considered method seems to be working, but there is one big BUT. Already for the “three by three” matrix, looking for eigenvalues is a long and unpleasant task; with a high probability you get a polynomial of the 3rd degree with irrational roots.
How to be? There is an easier way!
Sylvester's criterion
No, not Sylvester Stallone :) First, let me remind you what angular minors matrices. This determinants 
which "grow" from its upper left corner: 
and the last one is exactly equal to the determinant of the matrix.
Now, in fact, criterion:
1) Quadratic form defined positively if and only if ALL of its angular minors are greater than zero: .
2) Quadratic form defined negative if and only if its angular minors alternate in sign, while the 1st minor is less than zero: , , if is even or , if is odd.
If at least one angular minor has the opposite sign, then the form sign-alternating. If the angular minors are of “that” sign, but there are zeros among them, then this is a special case, which I will analyze a little later, after we click on more common examples.
Let us analyze the angular minors of the matrix 
:
And this immediately tells us that the form is not negatively determined.
Conclusion: all angle minors are greater than zero, so the shape 
positively defined.
Is there a difference with the eigenvalue method? ;)
We write the shape matrix from Example 1:
its first angular minor, and the second 
, whence it follows that the form is sign-alternating, i.e. depending on the values , can take both positive and negative values. However, this is so obvious.
Take the form and its matrix from Example 2:
here at all without insight not to understand. But with the Sylvester criterion, we don’t care:
, hence the form is definitely not negative.
, and definitely not positive. (because all angle minors must be positive).
Conclusion: the shape is alternating.
Warm-up examples for self-solving:
Example 4
Investigate quadratic forms for sign-definiteness
A) 
In these examples, everything is smooth (see the end of the lesson), but in fact, to complete such a task Sylvester's criterion may not be sufficient.
The point is that there are "boundary" cases, namely: if for any non-zero vector , then the shape is defined non-negative, if - then non-positive. These forms have non-zero vectors for which .
Here you can bring such a "button accordion":
Highlighting full square, we immediately see non-negativity form: , moreover, it is equal to zero for any vector with equal coordinates, for example: 
.
"Mirror" example non-positive certain form:
and an even more trivial example:
– here the form is equal to zero for any vector , where is an arbitrary number.
How to reveal the non-negativity or non-positiveness of a form?
For this we need the concept major minors
matrices. The main minor is a minor composed of elements that are at the intersection of rows and columns with the same numbers. So, the matrix has two principal minors of the 1st order:
(the element is at the intersection of the 1st row and 1st column);
(the element is at the intersection of the 2nd row and 2nd column),
and one major 2nd order minor: 
- composed of elements of the 1st, 2nd row and 1st, 2nd column.
Matrix "three by three" 
There are seven main minors, and here you already have to wave your biceps:
- three minors of the 1st order,
three minors of the 2nd order: 
- composed of elements of the 1st, 2nd row and 1st, 2nd column; 
- composed of elements of the 1st, 3rd row and 1st, 3rd column; 
- composed of elements of the 2nd, 3rd row and 2nd, 3rd column,
and one 3rd order minor: 
- composed of elements of the 1st, 2nd, 3rd row and 1st, 2nd and 3rd columns.
Exercise for understanding: write down all the main minors of the matrix 
.
We check at the end of the lesson and continue.
Schwarzenegger criterion:
1) Non-zero* quadratic form defined non-negative if and only if ALL of its principal minors non-negative(greater than or equal to zero).
* The zero (degenerate) quadratic form has all coefficients equal to zero.
2) Nonzero quadratic form with matrix defined non-positive if and only if its:
– principal minors of the 1st order non-positive(less than or equal to zero);
are principal minors of the 2nd order non-negative;
– principal minors of the 3rd order non-positive(alternation has begun);
…
– major minor of the th order non-positive, if is odd or non-negative, if is even.
If at least one minor is of the opposite sign, then the form is sign-alternating.
Let's see how the criterion works in the above examples:
Let's make a shape matrix, and Firstly let's calculate the angular minors - what if it is positively or negatively defined? 
The obtained values do not satisfy the Sylvester criterion, however, the second minor not negative, and this makes it necessary to check the 2nd criterion (in the case of the 2nd criterion, it will not be fulfilled automatically, i.e., a conclusion is immediately made about the sign alternation of the form).
Major minors of the 1st order:
- are positive
2nd order major minor: 
- not negative.
Thus, ALL major minors are non-negative, so the form non-negative.
Let's write the form matrix 
, for which, obviously, the Sylvester criterion is not satisfied. But we also did not receive opposite signs (because both angular minors are equal to zero). Therefore, we check the fulfillment of the criterion of non-negativity / non-positiveness. Major minors of the 1st order:
- not positive
2nd order major minor: 
- not negative.
Thus, according to the Schwarzenegger criterion (point 2), the form is determined non-positively.
Now, fully armed, we will analyze a more entertaining problem:
Example 5
Examine the quadratic form for sign-definiteness
This form is decorated with the order "alpha", which can be equal to any real number. But it'll only be more fun decide.
First, let's write down the form matrix, probably, many have already adapted to do it orally: on main diagonal we put the coefficients at the squares, and at the symmetrical places - the half coefficients of the corresponding "mixed" products:
Let's calculate the angular minors: 
I will expand the third determinant along the 3rd line:
In this section we will focus on a special but important class of positive quadratic forms.
Definition 3. A real quadratic form is called non-negative (non-positive) if for any real values of the variables
. (35)
In this case, the symmetric matrix of coefficients is called positive semidefinite (negative semidefinite).
Definition 4. A real quadratic form is called positive-definite (negative-definite) if for any real values of the variables that are not simultaneously equal to zero
. (36)
In this case, the matrix is also called positive definite (negative definite).
The class of positive-definite (negative-definite) forms is part of the class of non-negative (respectively, non-positive) forms.
Let a non-negative form be given. We represent it as a sum of independent squares:
. (37)
In this representation, all squares must be positive:
. (38)
Indeed, if there were any , then it would be possible to choose such values for which
But then, for these values of the variables, the form would have a negative value, which is impossible by the condition. Obviously, conversely, from (37) and (38) it follows that the form is positive.
Thus, a non-negative quadratic form is characterized by the equalities .
Let now be a positive definite form. Then also the non-negative form. Therefore, it can be represented in the form (37), where all are positive. It follows from the positive definiteness of the form that . Indeed, in the case it is possible to choose such values that are not simultaneously equal to zero, for which all would vanish. But then, by virtue of (37), at , which contradicts condition (36).
It is easy to see that, conversely, if in (37) and are all positive, then is a positive definite form.
In other words, a non-negative form is positive definite if and only if it is not singular.
The following theorem gives a criterion for the positive definiteness of a form in the form of inequalities that must be satisfied by the coefficients of the form. In this case, the notation already encountered in the previous sections for successive principal minors of the matrix is used:
.
Theorem 3. For a quadratic form to be positive definite, it is necessary and sufficient that the inequalities
Proof. The sufficiency of conditions (39) follows directly from the Jacobi formula (28). The necessity of conditions (39) is established as follows. From the positive definiteness of the form follows the positive definiteness of the "truncated" forms
.
But then all these forms must be non-singular, i.e.
Now we have the opportunity to use the Jacobi formula (28) (for ). Since on the right side of this formula all squares must be positive, then
This implies inequalities (39). The theorem has been proven.
Since any principal minor of a matrix, with proper renumbering of variables, can be placed in the upper left corner, we have
Consequence. In positive definite quadratic form, all principal minors of the coefficient matrix are positive:
Comment. From the non-negativity of successive principal minors
does not follow the non-negativity of the form . Indeed, the form
,
wherein 
, satisfies the conditions , but is not non-negative.
However, there is the following
Theorem 4. For a quadratic form to be non-negative, it is necessary and sufficient that all principal minors of its coefficient matrix be non-negative:
Proof. Let us introduce an auxiliary form that is nonpositive, it is necessary and sufficient that the inequalities
Related Articles
