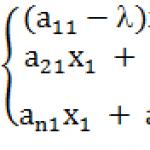Matrisnotationen för den kvadratiska formen har formen. Positiva bestämda kvadratiska former

Positiva bestämda kvadratiska former

Definition. Kvadratisk form från n okänd kallas positivt definitivt, om dess rang är lika med det positiva tröghetsindexet och är lika med antalet okända.

Sats. En kvadratisk form är positiv definitivt om och endast om den tar positiva värden på valfri uppsättning variabelvärden som inte är noll.

Bevis. Låt den kvadratiska formen vara en icke-degenererad linjär transformation av de okända

återgick till det normala

.

För varje uppsättning variabelvärden som inte är noll, minst ett av talen skiljer sig från noll, dvs. . Nödvändigheten av satsen är bevisad.

Antag att den kvadratiska formen tar positiva värden på alla variabler som inte är noll, men att dess tröghetsindex är positivt. Genom en icke-degenererad linjär transformation av de okända

Låt oss återställa det till det normala. Utan förlust av generalitet kan vi anta att i denna normala form saknas kvadraten på den sista variabeln antingen eller går in i den med ett minustecken, d.v.s. , var eller . Antag att det är en icke-noll uppsättning värden av variabler, erhållen som ett resultat av att lösa systemet med linjära ekvationer

I detta system är antalet ekvationer lika med antalet variabler och systemets determinant är icke-noll. Enligt Cramers teorem har systemet en unik lösning, och den är inte noll. För detta set. Motsägelse med tillståndet. Vi kommer fram till en motsägelse med antagandet, vilket bevisar satsens tillräcklighet.

Med detta kriterium är det inte möjligt att utifrån koefficienterna avgöra om en kvadratisk form är positiv-definitiv. Svaret på denna fråga ges av ett annat teorem, för vars formulering vi introducerar ytterligare ett begrepp. Huvudsaklig diagonal matris minderårigaär de minderåriga i dess övre vänstra hörn:

, , , … , .

Sats.En kvadratisk form är positiv definitivt om och endast om alla dess huvudsakliga diagonala mindretal är positiva.

Bevis vi kommer att utföra genom metoden för fullständig matematisk induktion på numret n kvadratiska formvariabler f.

Hypotes om induktion. Antag att för kvadratiska former med färre variabler n påståendet är korrekt.

Betrakta den kvadratiska formen från n variabler. Samla alla termer som innehåller i en parentes. De återstående termerna bildar en kvadratisk form i variabler. Enligt induktionshypotesen är påståendet sant för det.

Antag att den andragradsformen är positiv bestämd. Då är den andragradsformen också positiv bestämd. Om vi ​​antar att så inte är fallet, så finns det en uppsättning variabelvärden som inte är noll , för vilka och på motsvarande sätt, , vilket motsäger det faktum att den kvadratiska formen är positiv bestämd. Enligt induktionshypotesen är alla huvuddiagonala biroller av en kvadratisk form positiva, d.v.s. alla första biträden av kvadratisk form fär positiva. Sista huvudsakliga biämne av andragradsform – är determinanten för dess matris. Denna determinant är positiv, eftersom dess tecken sammanfaller med tecknet för matrisen i dess normala form, dvs. med tecknet för identitetsmatrisdeterminanten.

Låt alla huvuddiagonalmolor i kvadratformen vara positiva. Då är alla huvuddiagonalamolorer av kvadratiska formen positiva från likheten . Enligt induktionshypotesen är den kvadratiska formen positiv bestämd, så det finns en icke-degenererad linjär transformation av variabler som reducerar formen till formen av summan av kvadrater av nya variabler. Denna linjära transformation kan utökas till en icke degenererad linjär transformation av alla variabler genom att ställa in . Den kvadratiska formen reduceras genom denna transformation till formen

Konceptet med en kvadratisk form. Matris av kvadratisk form. Kanonisk form av en kvadratisk form. Lagrange metod. Den normala formen av en kvadratisk form. Rang, index och signatur av en kvadratisk form. Positiv bestämd kvadratisk form. Quadris.

Konceptet med en kvadratisk form: en funktion på ett vektorrum som ges av ett homogent polynom av andra graden i vektorns koordinater.

kvadratisk form från n okänd kallas summan, vars termer är antingen kvadraten på en av dessa okända, eller produkten av två olika okända.

Kvadratisk matris: Matrisen kallas matrisen av kvadratisk form i den givna basen. Om fältkarakteristiken inte är lika med 2 kan vi anta att matrisen för den kvadratiska formen är symmetrisk, det vill säga .

Skriv en matris av kvadratisk form:

Därav,

I vektormatrisform är den kvadratiska formen:

A, var

Kanonisk form av en kvadratisk form: En kvadratisk form kallas kanonisk om alla dvs.

Vilken kvadratisk form som helst kan reduceras till en kanonisk form med hjälp av linjära transformationer. I praktiken används vanligtvis följande metoder.

Lagrange metod : successivt urval av hela rutor. Till exempel om

Sedan görs en liknande procedur med den kvadratiska formen etc. Om i kvadratisk form allt men är sedan, efter en preliminär omvandling, reduceras ärendet till det övervägda förfarandet. Således, om, till exempel, då vi sätter

Den normala formen av en kvadratisk form är: En normal kvadratisk form är en kanonisk kvadratisk form där alla koefficienter är lika med +1 eller -1.

Rang, index och signatur för en kvadratisk form: Rangen för den kvadratiska formen A kallas matrisens rangordning A. Rangen för en kvadratisk form ändras inte under icke degenererade transformationer av okända.

Antalet negativa koefficienter kallas det negativa formindexet.

Antalet positiva termer i den kanoniska formen kallas det positiva tröghetsindexet för den kvadratiska formen, antalet negativa termer kallas det negativa indexet. Skillnaden mellan positiva och negativa index kallas den kvadratiska formens signatur

Positiv bestämd kvadratisk form: Verklig kvadratisk form kallas positiv-definitiv (negativ-definitiv) om för några reella värden av variablerna som inte samtidigt är lika med noll

. (36)

I det här fallet kallas matrisen också positiv definit (negativ definit).

Klassen av positiv-definita (negativ-definita) former är en del av klassen av icke-negativa (respektive icke-positiva) former.

Fyrhjulingar: Quadric - n-dimensionell hyperyta in n+1-dimensionellt rymd, definierat som mängden nollor i ett polynom av andra graden. Om du anger koordinaterna ( x 1 , x 2 , x n+1 ) (i euklidiskt eller affint rymd), den allmänna kvadratiska ekvationen har formen

Denna ekvation kan skrivas om mer kompakt i matrisnotation:

där x = ( x 1 , x 2 , x n+1) är en radvektor, x T är den transponerade vektorn, Fär storleksmatrisen ( n+1)×( n+1) (det antas att minst ett av dess element inte är noll), Pär en radvektor, och Rär en konstant. Oftast betraktas kvadricker över reella eller komplexa tal. Definitionen kan utvidgas till quadrics i projektivt rum, se nedan.

Mer allmänt är uppsättningen av nollor i ett system av polynomekvationer känd som en algebraisk variant. Således är en kvadric en (affin eller projektiv) algebraisk variant av andra graden och kodimension 1.

Plan- och rymdtransformationer.

Definition av plantransformation. Definition av rörelse. rörelseegenskaper. Två typer av rörelser: rörelse av det första slaget och rörelse av det andra slaget. Rörelseexempel. Analytiskt uttryck av rörelse. Klassificering av planrörelser (beroende på närvaron av fasta punkter och invarianta linjer). Grupp av planrörelser.

Plantransformationsdefinition: Definition. En plantransformation som bevarar avståndet mellan punkter kallas rörelse(eller förskjutning) av planet. Plantransformationen kallas affin, om det tar några tre punkter som ligger på samma linje till tre punkter som också ligger på samma linje och samtidigt bevarar den enkla relationen mellan de tre punkterna.

Rörelsedefinition: Detta är en formtransformation som bevarar avstånden mellan punkter. Om två figurer är exakt kombinerade med varandra genom rörelse, så är dessa figurer lika, lika.

Rörelseegenskaper: varje orienteringsbevarande rörelse av ett plan är antingen en parallell translation eller en rotation; varje orienteringsförändrande rörelse av ett plan är antingen en axiell symmetri eller en glidsymmetri. Punkter som ligger på en rak linje, när de rör sig, övergår i punkter som ligger på en rak linje, och ordningen för deras inbördes arrangemang bevaras. Vid förflyttning bevaras vinklarna mellan halvlinjerna.

Två typer av rörelser: rörelse av det första slaget och rörelse av det andra slaget: Rörelser av det första slaget är de rörelser som bevarar orienteringen av baserna för en viss figur. De kan realiseras med kontinuerliga rörelser.

Rörelser av det andra slaget är de rörelser som ändrar orienteringen av baserna till den motsatta. De kan inte realiseras genom kontinuerliga rörelser.

Exempel på rörelser av det första slaget är translation och rotation runt en rät linje, och rörelser av det andra slaget är centrala och spegelsymmetrier.

Sammansättningen av valfritt antal rörelser av det första slaget är en rörelse av det första slaget.

Sammansättningen av ett jämnt antal satser av andra slaget är en sats av 1:a slaget, och sammansättningen av ett udda antal satser av 2:a slaget är en sats av 2:a slaget.

Exempel på rörelser:Parallell överföring. Låt a vara en given vektor. Parallell överföring till vektorn a är avbildningen av planet på sig själv, där varje punkt M mappas till punkten M 1, att vektorn MM 1 är lika med vektorn a.

Parallellöversättning är en rörelse eftersom det är en kartläggning av planet på sig själv, vilket bevarar avstånd. Visuellt kan denna rörelse representeras som en förskjutning av hela planet i riktningen för en given vektor a med dess längd.

Sväng . Låt oss beteckna en punkt O på planet ( vändcentrum) och ställ in vinkeln α ( rotationsvinkel). Rotationen av planet runt punkten O med vinkeln α är avbildningen av planet på sig själv, där varje punkt M mappas till punkten M 1, att OM = OM 1 och vinkeln MOM 1 är lika med α. I det här fallet förblir punkten O på sin plats, d.v.s. den visas i sig själv, och alla andra punkter roterar runt punkten O i samma riktning - medurs eller moturs (bilden visar en moturs rotation).

En sväng är en rörelse eftersom det är en kartläggning av planet på sig själv, vilket bevarar avstånd.

Analytiskt uttryck för rörelse: det analytiska sambandet mellan koordinaterna för förbilden och bilden av punkten har formen (1).

Klassificering av planrörelser (beroende på närvaron av fixpunkter och invarianta linjer): Definition:

En punkt i ett plan är invariant (fixerad) om den under en given transformation transformerar till sig själv.

Exempel: Med central symmetri är punkten för symmetricentrum invariant. Vid svängning är rotationscentrumets punkt oföränderlig. Med axiell symmetri är linjen invariant - symmetriaxeln är linjen med invarianta punkter.

Sats: Om rörelsen inte har någon invariant punkt, så har den minst en invariant riktning.

Exempel: Parallellöverföring. Linjer parallella med denna riktning är faktiskt invarianta som en figur som helhet, även om den inte består av invarianta punkter.

Teorem: Om någon stråle rör sig översätts strålen till sig själv, då är denna rörelse antingen en identisk transformation eller en symmetri med avseende på linjen som innehåller den givna strålen.

Därför, enligt närvaron av oföränderliga punkter eller figurer, är det möjligt att klassificera rörelser.

Rörelsens namn	Invarianta poäng	Invarianta linjer
Rörelse av det första slaget.
1. - sväng	(mitten) - 0	Nej
2. Identitetsförvandling	alla punkter på planet	allt rakt
3. Central symmetri	punkt 0 - mitten	alla linjer som går genom punkt 0
4. Parallellöverföring	Nej	allt rakt
Rörelse av det andra slaget.
5. Axialsymmetri.	uppsättning punkter	symmetriaxel (rak) allt rakt

Flygplansrörelsegrupp: Inom geometrin spelar självsammanfallsgrupper av figurer en viktig roll. Om - någon figur på planet (eller i rymden), så kan vi betrakta uppsättningen av alla dessa rörelser i planet (eller rymden), där figuren passerar in i sig själv.

Denna uppsättning är en grupp. Till exempel, för en liksidig triangel består gruppen av planrörelser som tar triangeln in i sig av 6 element: rotationer med vinklar runt en punkt och symmetrier kring tre linjer.

De visas i fig. 1 med röda streck. Elementen i gruppen med självsammanfall i en vanlig triangel kan specificeras på annat sätt. För att förtydliga detta, låt oss numrera hörnen i en vanlig triangel med siffrorna 1, 2, 3. kan villkorligt anges i form av en av dessa parenteser:

etc.

där siffrorna 1, 2, 3 anger numren på de hörn som hörn 1, 2, 3 passerar som ett resultat av den övervägda rörelsen.

Projektiva rum och deras modeller.

Begreppet projektivt utrymme och modell av projektivt utrymme. Grundläggande fakta om projektiv geometri. Ett gäng linjer centrerade vid punkt O är en projektiv planmodell. projektiva punkter. Det förlängda planet är en modell av det projektiva planet. En utökad tredimensionell affin eller euklidisk rymd är en projektiv rymdmodell. Bilder av plana och rumsliga figurer i parallell design.

Begreppet projektivt utrymme och modell av projektivt utrymme:

Ett projektivt utrymme över ett fält är ett utrymme som består av linjer (endimensionella delrum) av något linjärt utrymme över ett givet fält. De raka utrymmena kallas prickar projektivt utrymme. Denna definition lämpar sig för generalisering till ett godtyckligt organ

Om den har dimension kallas det projektiva utrymmets dimension numret och själva det projektiva utrymmet betecknas och kallas associerat med (för att indikera detta antas notationen).

Övergången från ett vektorrum av dimension till motsvarande projektiva rum kallas projektivisering mellanslag.

Punkter kan beskrivas med hjälp av homogena koordinater.

Grundläggande fakta om projektiv geometri: Projektiv geometri är en gren av geometri som studerar projektiva plan och rum. Huvuddraget i projektiv geometri är principen om dualitet, som lägger till en graciös symmetri till många mönster. Projektiv geometri kan studeras både från en rent geometrisk synvinkel och från en analytisk (med hjälp av homogena koordinater) och salgebraisk synvinkel, med tanke på det projektiva planet som en struktur över ett fält. Ofta, och historiskt sett, behandlas det verkliga projektiva planet som det euklidiska planet med tillägget av en "linje i oändligheten".

Medan egenskaperna hos de figurer som den euklidiska geometrin behandlar är metrisk(specifika värden för vinklar, segment, ytor), och siffrornas ekvivalens är ekvivalent med deras kongruens(dvs när figurer kan översättas till varandra med hjälp av rörelse samtidigt som metriska egenskaper bevaras), finns det mer "djupare" egenskaper hos geometriska figurer som bevaras genom transformationer av en mer allmän typ än rörelse. Projektiv geometri studerar egenskaperna hos figurer som är invarianta under klassen projektiva transformationer, såväl som dessa transformationer i sig.

Projektiv geometri kompletterar Euklidisk genom att tillhandahålla vackra och enkla lösningar på många problem som kompliceras av närvaron av parallella linjer. Den projektiva teorin om koniska sektioner är särskilt enkel och elegant.

Det finns tre huvudsakliga tillvägagångssätt för projektiv geometri: oberoende axiomatisering, tillägg till euklidisk geometri och struktur över ett fält.

Axiomatisering

Ett projektivt utrymme kan definieras med en annan uppsättning axiom.

Coxeter tillhandahåller följande:

1. Det finns en linje och en punkt finns inte på den.

2. Det finns minst tre punkter på varje linje.

3. Exakt en rät linje kan dras genom två punkter.

4. Om A, B, C, Och D olika punkter och AB Och CD skära, alltså AC Och BD korsas.

5. Om ABCär ett plan, så finns det åtminstone en punkt som inte finns i planet ABC.

6. Två distinkta plan skär varandra i minst två punkter.

7. Tre diagonala punkter på en hel fyrhörning är inte kolinjära.

8. Om det finns tre punkter på en rak linje X X

Det projektiva planet (utan den tredje dimensionen) definieras av något olika axiom:

1. Exakt en rät linje kan dras genom två punkter.

2. Alla två linjer skär varandra.

3. Det finns fyra punkter, av vilka det inte finns tre kolinjära.

4. Tre diagonala punkter av kompletta fyrhörningar är inte kolinjära.

5. Om det finns tre punkter på en rak linje Xär invarianta under projektiviteten av φ, sedan alla punkter på Xär invarianta med avseende på φ.

6. Desargues sats: Om två trianglar är perspektiv genom en punkt, så är de perspektiv genom en linje.

I närvaro av en tredje dimension kan Desargues sats bevisas utan att introducera den ideala punkten och linjen.

Utökat plan - projektiv planmodell: i ett affint utrymme A3, ta ett knippe av linjer S(O) centrerade i en punkt O och ett plan Π som inte går genom buntens centrum: O 6∈ Π. Ett knippe linjer i ett affint utrymme är en modell av det projektiva planet. Låt oss ställa in kartläggningen av uppsättningen av punkter i planet Π till uppsättningen av linjer i bunten S (Fan, be om du har den här frågan, jag är ledsen)

Utökad tredimensionell affin eller euklidisk rymd - projektiv rymdmodell:

För att göra kartläggningen surjektiv upprepar vi processen att formellt utöka det affina planet Π till det projektiva planet, Π, och komplettera planet Π med en uppsättning felaktiga punkter (M∞) så att: ((M∞)) = PO(O). Eftersom den omvända bilden av varje plan av planknippet S(O) i kartläggningen är en linje på planet d, är det uppenbart att mängden av alla felaktiga punkter i det förlängda planet: Π = Π ∩ (M∞) , (M∞), är en felaktig linje d∞ i det förlängda planet som är den omvända bilden av singularplanet Π0: (d∞) = P0(O) (= Π0). (I.23) Låt oss komma överens om att vi här och nedan kommer att förstå den sista likheten P0(O) = Π0 i betydelsen likhet mellan uppsättningar av poäng, men utrustad med olika strukturer. Genom att komplettera det affina planet med en felaktig linje, har vi sett till att avbildningen (I.21) blir bijektiv på uppsättningen av alla punkter i det utökade planet:

Bilder av platta och rumsliga figurer i parallell design:

Inom stereometri studeras rumsliga figurer, men på ritningen avbildas de som platta figurer. Hur ska då en rumslig figur avbildas på ett plan? Vanligtvis i geometri används parallell design för detta. Låt p vara något plan, l- en rät linje som skär den (fig. 1). Genom en godtycklig punkt A, som inte tillhör linjen l dra en linje parallellt med linjen l. Skärningspunkten för denna linje med planet p kallas parallellprojektion av punkten A till planet p i riktning mot den räta linjen l. Låt oss beteckna det A". Om poängen A tillhör linjen l, sedan parallellprojektionen A till planet p betraktas som skärningspunkten för linjen l med plan sid.

Alltså varje punkt A rymden mappas till dess projektion A" på planet p. Denna överensstämmelse kallas den parallella projektionen på planet p i den räta linjens riktning l.

Grupp av projektiva transformationer. Applikation för problemlösning.

Begreppet projektiv omvandling av planet. Exempel på projektiva plantransformationer. Egenskaper för projektiva transformationer. Homologi, egenskaper hos homologi. Grupp av projektiva transformationer.

Konceptet med en projektiv plantransformation: Föreställningen om en projektiv transformation generaliserar föreställningen om en central projektion. Om vi ​​utför den centrala projektionen av planet α på något plan α 1 , då projektionen av α 1 på α 2 , α 2 på α 3 , ... och, slutligen, något plan α nåterigen på α 1 är sammansättningen av alla dessa projektioner den projektiva transformationen av planet α; en sådan kedja kan innefatta parallella projektioner.

Exempel på projektiva plantransformationer: En projektiv transformation av ett förstärkt plan är dess en-till-en-mappning på sig själv, vilket bevarar kollineariteten hos punkter, eller, med andra ord, bilden av en rät linje är en rät linje. Varje projektiv transformation är en sammansättning av en kedja av centrala och parallella projektioner. En affin transformation är ett specialfall av en projektiv, där linjen i oändligheten går in i sig själv.

Egenskaper för projektiva transformationer:

Under en projektiv transformation mappas tre punkter som inte ligger på en linje till tre punkter som inte ligger på en linje.

Under en projektiv transformation går ramen över till ramen.

Under en projektiv transformation går en linje in i en rak linje, en kärve går in i en kärve.

Homologi, homologiegenskaper:

En projektiv transformation av ett plan som har en linje av invarianta punkter och därmed en penna av invarianta linjer kallas homologi.

1. En linje som går genom motsvarande icke-sammanfallande homologipunkter är en invariant linje;

2. Linjerna som går genom motsvarande icke-sammanfallande homologipunkter tillhör samma penna, vars centrum är en invariant punkt.

3. En punkt, dess bild och homologins centrum ligger på samma räta linje.

Grupp av projektiva transformationer: betrakta en projektiv avbildning av det projektiva planet P 2 på sig självt, det vill säga en projektiv transformation av detta plan (P 2 ' = P 2).

Liksom tidigare är sammansättningen f av projektiva transformationer fi och f2 av det projektiva planet P2 resultatet av successiv utförande av transformationer fi och f2: f = f2°f1.

Sats 1: Mängden H för alla projektiva transformationer av det projektiva planet P 2 är en grupp under sammansättningen av projektiva transformationer.

Kvadratiska former

kvadratisk form f(x 1, x 2,..., x n) av n variabler kallas summan, vars termer är antingen kvadraten på en av variablerna, eller produkten av två olika variabler, tagna med en viss koefficient: f(x 1, x 2, ...,x n) = (a ij = a ji).

Matrisen A, som består av dessa koefficienter, kallas kvadratisk formmatris. Det är alltid symmetrisk matris (d.v.s. en matris symmetrisk kring huvuddiagonalen, a ij = a ji).

I matrisnotation har den andragradsformen formen f(X) = X T AX, där

Verkligen

Låt oss till exempel skriva kvadratisk form i matrisform.

För att göra detta hittar vi en matris av en kvadratisk form. Dess diagonala element är lika med koefficienterna vid variablernas kvadrater, och de återstående elementen är lika med hälften av motsvarande koefficienter i kvadratformen. Det är därför

Låt matriskolumnen för variablerna X erhållas genom en icke-degenererad linjär transformation av matriskolumnen Y, dvs. X = CY, där C är en icke-degenererad matris av ordningen n. Sedan den kvadratiska formen
f(X) \u003d X T AX \u003d (CY) T A (CY) \u003d (Y T C T) A (CY) \u003d Y T (C T AC) Y.

Sålunda, under en icke-degenererad linjär transformation C, antar matrisen av den kvadratiska formen formen: A * = C T AC.

Låt oss till exempel hitta den kvadratiska formen f(y 1, y 2) som erhålls från den kvadratiska formen f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 genom en linjär transformation.

Den kvadratiska formen kallas kanonisk(Det har kanonisk syn) om alla dess koefficienter a ij = 0 för i ≠ j, dvs.
f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + ... + a nn x n 2 = .

Dess matris är diagonal.

Sats(beviset ges inte här). Vilken kvadratisk form som helst kan reduceras till en kanonisk form med hjälp av en icke-degenererad linjär transformation.

Låt oss till exempel reducera den kvadratiska formen till den kanoniska formen
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

För att göra detta, välj först hela kvadraten för variabeln x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Nu väljer vi hela kvadraten för variabeln x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 - 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) - (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 - (1/20) x 3 2.

Sedan en icke-degenererad linjär transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 - (1/10) x 3 och y 3 \u003d x 3 för denna kvadratiska form till den kanoniska formen f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 - (1/20) y 3 2 .

Observera att den kanoniska formen av en kvadratisk form definieras tvetydigt (samma kvadratiska form kan reduceras till den kanoniska formen på olika sätt). Kanoniska former erhållna med olika metoder har dock ett antal gemensamma egenskaper. Särskilt antalet termer med positiva (negativa) koefficienter av en kvadratisk form beror inte på hur formen reduceras till denna form (till exempel i det övervägda exemplet kommer det alltid att finnas två negativa och en positiv koefficient). Denna egenskap kallas tröghetslagen för kvadratiska former.

Låt oss verifiera detta genom att reducera samma kvadratiska form till den kanoniska formen på ett annat sätt. Låt oss börja transformationen med variabeln x 2:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 -
- 2 * x 2 ((1/6) x 3 + (2/3) x 1) + ((1/6) x 3 + (2/3) x 1) 2) - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 - (1/6) x 3 - (2/3) x 1) 2 - 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2, där y 1 \u003d - (2/3) x 1 + x 2 - (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 och y3 = x 1 . Här en positiv koefficient 2 för y 3 och två negativa koefficienter (-3) för y 1 och y 2 (och med en annan metod fick vi en positiv koefficient 2 för y 1 och två negativa koefficienter - (-5) för y 2 och (-1/20) för y 3).

Det bör också noteras att rangordningen av en matris av en kvadratisk form, kallas den andragradsformens rangordning, är lika med antalet koefficienter som inte är noll för den kanoniska formen och ändras inte under linjära transformationer.

Andragradsformen f(X) kallas positivt (negativ) vissa, om för alla värden av variablerna som inte samtidigt är lika med noll, är det positivt, dvs. f(X) > 0 (negativ, dvs.
f(X)< 0).

Till exempel är kvadratformen f 1 (X) \u003d x 1 2 + x 2 2 positiv definitiv, eftersom är summan av kvadrater, och den kvadratiska formen f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 är negativ definitiv, eftersom representerar det kan representeras som f 2 (X) \u003d - (x 1 - x 2) 2.

I de flesta praktiska situationer är det något svårare att fastställa teckendefiniiteten för en kvadratisk form, så en av följande satser används för detta (vi formulerar dem utan bevis).

Sats. En kvadratisk form är positiv (negativ) definitiv om och endast om alla egenvärden i dess matris är positiva (negativa).

Sats (Sylvesters kriterium). En kvadratisk form är positiv definitivt om och endast om alla huvudbiträden i matrisen för denna form är positiva.

Major (hörn) moll Den k:te ordningen av matrisen A av den n:te ordningen kallas matrisens determinant, sammansatt av de första k raderna och kolumnerna i matrisen A ().

Observera att för negativ-definita andragradsformer alternerar tecknen för de huvudsakliga minderåriga, och den första ordningens moll måste vara negativ.

Till exempel undersöker vi den kvadratiska formen f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 för teckendefiniitet.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
. Därför är den kvadratiska formen positiv bestämd.

Metod 2. Main moll av första ordningen av matrisen A D 1 = a 11 = 2 > 0. Main moll av andra ordningen D 2 = = 6 - 4 = 2 > 0. Därför, enligt Sylvester-kriteriet, den andragradsformen är positiv bestämd.

Vi undersöker en annan kvadratisk form för teckendefiniitet, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metod 1. Låt oss konstruera en matris med kvadratisk form А = . Den karakteristiska ekvationen kommer att ha formen = (-2 - l)*
*(-3 - l) - 4 \u003d (6 + 2l + 3l + l 2) - 4 \u003d l 2 + 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
. Därför är den kvadratiska formen negativ bestämd.

Fyrkantiga former.
Formernas betydelse. Sylvesters kriterium

Adjektivet "kvadrat" antyder omedelbart att något här är kopplat till en kvadrat (andra graden), och mycket snart kommer vi att veta detta "något" och vad en form är. Det visade sig direkt :)

Välkommen till min nya lektion, och som en omedelbar uppvärmning ska vi titta på den randiga formen linjär. Linjär form variabler kallad homogen 1:a gradens polynom:

- några specifika siffror * (vi antar att minst en av dem skiljer sig från noll), och är variabler som kan ta godtyckliga värden.

* I det här ämnet kommer vi bara att överväga riktiga nummer .

Vi har redan stött på termen "homogen" i lektionen om homogena system av linjära ekvationer, och i det här fallet innebär det att polynomet inte har en adderad konstant.

Till exempel: – linjär form av två variabler

Nu är formen kvadratisk. kvadratisk form variabler kallad homogen 2:a gradens polynom, varav varje termin innehåller antingen kvadraten på variabeln eller dubbel produkt av variabler. Så till exempel har den kvadratiska formen av två variabler följande form:

Uppmärksamhet! Detta är en standardpost och du behöver inte ändra något i den! Trots det "hemska" utseendet är allt enkelt här - dubbla nedskrivningar av konstanter signalerar vilka variabler som ingår i en eller annan term:
– denna term innehåller produkten och (fyrkantig);
- här är arbetet;
- och här är arbetet.

- Jag förutser omedelbart ett grovt misstag när de tappar "minus" på koefficienten, utan att inse att det syftar på termen:

Ibland finns det en "skola"-version av designen i andan, men då bara ibland. Observera förresten att konstanterna här inte säger oss något alls, och därför är det svårare att komma ihåg den "enkla notationen". Speciellt när det finns fler variabler.

Och den kvadratiska formen av tre variabler innehåller redan sex termer:

... varför sätts "två" multiplikatorer i "blandade" termer? Detta är bekvämt, och det kommer snart att stå klart varför.

Men vi kommer att skriva ner den allmänna formeln, det är bekvämt att ordna det med ett "ark":

- studera noga varje rad - det är inget fel med det!

Den kvadratiska formen innehåller termer med kvadratiska variabler och termer med deras parprodukter (centimeter. kombinatorisk formel för kombinationer) . Inget annat - inget "ensamt x" och ingen adderad konstant (då får du inte en kvadratisk form, men heterogen 2:a gradens polynom).

Matrisnotation av en kvadratisk form

Beroende på värdena kan den betraktade formen ha både positiva och negativa värden, och detsamma gäller för vilken linjär form som helst - om åtminstone en av dess koefficienter är icke-noll, kan den visa sig vara antingen positiv eller negativ (beroende på värdena) på värderingar).

Denna form kallas omväxlande. Och om allt är transparent med den linjära formen, är saker och ting mycket mer intressanta med den kvadratiska formen:

Det är helt klart att denna form kan anta värdena för vilket tecken som helst, alltså, den kvadratiska formen kan också vara alternerande.

Det kanske inte är:

– alltid, om inte båda är lika med noll.

- för vem som helst vektor förutom noll.

Och generellt sett, om för någon icke-noll vektor , , då kallas den kvadratiska formen positivt definitivt; om då negativt definitivt.

Och allt skulle vara bra, men bestämningen av den kvadratiska formen är endast synlig i enkla exempel, och denna synlighet går förlorad redan med en liten komplikation:
– ?

Man kan anta att formen är positivt definierad, men är det verkligen så? Plötsligt finns det värden där det är mindre än noll?

På detta konto, där sats: Om alla egenvärden matriser av kvadratisk form är positiva * , då är det positivt definierat. Om alla är negativa så är det negativa.

* Det är bevisat i teorin att alla egenvärden för en verklig symmetrisk matris giltig

Låt oss skriva matrisen för ovanstående form:
och från ekvationen låt oss hitta henne egenvärden:

Vi löser det gamla goda andragradsekvation:

, alltså formen är positivt definierad, dvs. för alla värden som inte är noll är det större än noll.

Den övervägda metoden verkar fungera, men det finns ett stort MEN. Redan för matrisen "tre av tre" är det en lång och obehaglig uppgift att leta efter egenvärden; med hög sannolikhet får man ett polynom av 3:e graden med irrationella rötter.

Hur man är? Det finns ett enklare sätt!

Sylvesters kriterium

Nej, inte Sylvester Stallone :) Låt mig först påminna dig om vad kantiga minderåriga matriser. Detta determinanter som "växer" från dess övre vänstra hörn:

och den sista är exakt lika med matrisens determinant.

Nu, faktiskt, kriterium:

1) Kvadratisk form definierad positivt om och endast om ALLA dess vinkelformiga mindre är större än noll: .

2) Kvadratisk form definierad negativ om och endast om dess kantiga moll alternerar i tecken, medan 1:a moll är mindre än noll: , , om är jämnt eller , om är udda.

Om minst en kantig moll har motsatt tecken, då formen tecken växlande. Om de kantiga minderåriga är av "det" tecknet, men det finns nollor bland dem, är detta ett specialfall, som jag kommer att analysera lite senare, efter att vi klickat på vanligare exempel.

Låt oss analysera de vinkelformiga minorerna i matrisen :

Och detta säger oss genast att formen inte är negativt bestämd.

Slutsats: alla vinkel mindre är större än noll, så formen positivt definierad.

Finns det någon skillnad med egenvärdesmetoden? ;)

Vi skriver formmatrisen från Exempel 1:

dess första kantiga moll och den andra , därav följer att formen är teckenväxlande, d.v.s. beroende på värden, kan ta både positiva och negativa värden. Detta är dock så uppenbart.

Ta formen och dess matris från Exempel 2:

här överhuvudtaget utan insikt att inte förstå. Men med Sylvester-kriteriet bryr vi oss inte:
, därför är formen definitivt inte negativ.

, och definitivt inte positivt. (eftersom alla vinkel minderåriga måste vara positiva).

Slutsats: formen är omväxlande.

Uppvärmningsexempel för självlösning:

Exempel 4

Undersök kvadratiska former för teckendefiniitet

A)

I dessa exempel är allt smidigt (se slutet av lektionen), men i själva verket att slutföra en sådan uppgift Sylvesters kriterium kanske inte är tillräckligt.

Poängen är att det finns "gränsfall", nämligen: om för några icke-noll vektor , då definieras formen icke-negativ, om då icke-positiva. Dessa former har icke-noll vektorer för vilka .

Här kan du ta med ett sådant "knappdragspel":

Markering hel fyrkant, ser vi genast icke-negativitet form: dessutom är det lika med noll för alla vektorer med lika koordinater, till exempel: .

Exempel på "spegel". icke-positiva viss form:

och ett ännu mer trivialt exempel:
– här är formen lika med noll för vilken vektor som helst , där är ett godtyckligt tal.

Hur avslöjar man icke-negativiteten eller icke-positiviteten hos en form?

För detta behöver vi konceptet större minderåriga matriser. Huvudmoll är en moll som består av element som är i skärningspunkten mellan rader och kolumner med samma nummer. Så, matrisen har två huvudsakliga mindreåriga av 1:a ordningen:
(elementet är i skärningspunkten mellan den första raden och den första kolumnen);
(elementet är i skärningspunkten mellan den andra raden och den andra kolumnen),

och en stor 2:a ordningens moll:
- består av element i första, andra raden och första, andra kolumnen.

Matris "tre och tre" Det finns sju huvudsakliga minderåriga, och här måste du redan vifta med dina biceps:
- tre minderåriga av första ordningen,
tre minderåriga av andra ordningen:
- består av element i första, andra raden och första, andra kolumnen;
- består av element i första, tredje raden och första, tredje kolumnen;
- sammansatt av element i 2:a, 3:e raden och 2:a, 3:e kolumnen,
och en 3:e ordningens moll:
- består av element i 1:a, 2:a, 3:e raden och 1:a, 2:a och 3:e kolumnen.
Träning för förståelse: skriv ner alla de viktigaste minorerna i matrisen .
Vi kollar i slutet av lektionen och fortsätter.

Schwarzenegger kriterium:

1) Andragradsform som inte är noll* definierad icke-negativ om och bara om ALLA dess huvudsakliga minderåriga icke-negativ(större än eller lika med noll).

* Den noll (degenererade) kvadratiska formen har alla koefficienter lika med noll.

2) Andragradsform som inte är noll med matris definierad icke-positiva om och bara om det är:
– främst minderåriga av 1:a ordningen icke-positiva(mindre än eller lika med noll);
är främst minderåriga av 2:a ordningen icke-negativ;
– främst minderåriga av 3:e ordningen icke-positiva(växlingen har börjat);
…
– moll major av th ordningen icke-positiva, om är udda eller icke-negativ, om är jämnt.

Om minst en minderårig har motsatt tecken, är formen teckenväxlande.

Låt oss se hur kriteriet fungerar i exemplen ovan:

Låt oss göra en formmatris, och för det första låt oss beräkna de vinkelformiga minorerna - vad händer om det är positivt eller negativt definierat?

De erhållna värdena uppfyller inte Sylvester-kriteriet, men den andra mindre inte negativ, och detta gör det nödvändigt att kontrollera det andra kriteriet (när det gäller det andra kriteriet kommer det inte att uppfyllas automatiskt, d.v.s. en slutsats görs omedelbart om teckenväxlingen av formen).

Större minderåriga av 1:a ordningen:
- är positiva
2:a ordningens major-moll:
- inte negativt.

Alltså är ALLA större minderåriga icke-negativa, så formen icke-negativ.

Låt oss skriva formmatrisen , för vilket Sylvester-kriteriet uppenbarligen inte är uppfyllt. Men vi fick inte heller motsatta tecken (eftersom båda kantiga minorerna är lika med noll). Därför kontrollerar vi uppfyllandet av kriteriet icke-negativitet / icke-positivitet. Större minderåriga av 1:a ordningen:
– inte positivt
2:a ordningens major-moll:
- inte negativt.

Enligt Schwarzenegger-kriteriet (punkt 2) bestäms alltså formen icke-positivt.

Nu, fullt beväpnade, kommer vi att analysera ett mer underhållande problem:

Exempel 5

Undersök den andragradsformen för teckendefiniitet

Denna form är dekorerad med ordningen "alfa", som kan vara lika med vilket reellt tal som helst. Men det blir bara roligare besluta.

Låt oss först skriva ner formmatrisen, förmodligen har många redan anpassat sig för att göra det muntligt: ​​på huvuddiagonal vi sätter koefficienterna vid kvadraterna och på de symmetriska platserna - halvkoefficienterna för motsvarande "blandade" produkter:

Låt oss beräkna de vinkelformiga minorerna:

Jag kommer att utöka den tredje determinanten längs den tredje raden:

I detta avsnitt kommer vi att fokusera på en speciell men viktig klass av positiva kvadratiska former.

Definition 3. En reell kvadratisk form kallas icke-negativ (icke-positiv) om för några reella värden av variablerna

. (35)

I detta fall kallas den symmetriska matrisen av koefficienter positiv semidefinite (negativ semidefinite).

Definition 4. En reell kvadratisk form kallas positiv-definit (negativ-definitiv) om det för några reella värden av variablerna inte samtidigt är lika med noll

. (36)

I det här fallet kallas matrisen också positiv definit (negativ definit).

Klassen av positiv-definita (negativ-definita) former är en del av klassen av icke-negativa (respektive icke-positiva) former.

Låt en icke-negativ form ges. Vi representerar det som en summa av oberoende kvadrater:

. (37)

I denna representation måste alla rutor vara positiva:

. (38)

Faktum är att om det fanns några, skulle det vara möjligt att välja sådana värden för vilka

Men då, för dessa värden av variablerna, skulle formen ha ett negativt värde, vilket är omöjligt av villkoret. Uppenbarligen, omvänt, av (37) och (38) följer att formen är positiv.

Således kännetecknas en icke-negativ kvadratisk form av likheterna .

Låt nu vara en positiv bestämd form. Sedan även den icke-negativa formen. Därför kan det representeras i formen (37), där alla är positiva. Av formens positiva bestämdhet följer att . I själva verket är det möjligt att välja sådana värden som inte samtidigt är lika med noll, för vilka alla skulle försvinna. Men då, i kraft av (37), vid , som motsäger villkor (36).

Det är lätt att se att omvänt, om i (37) och alla är positiva, så är det en positiv bestämd form.

Med andra ord är en icke-negativ form positiv definitiv om och endast om den inte är singular.

Följande sats ger ett kriterium för en forms positiva definititet i form av ojämlikheter som måste uppfyllas av formens koefficienter. I det här fallet används notationen som redan påträffats i de föregående avsnitten för på varandra följande underåriga i matrisen:

.

Sats 3. För att en kvadratisk form ska vara positiv definitiv är det nödvändigt och tillräckligt att ojämlikheterna

Bevis. Tillräckligheten av villkor (39) följer direkt av Jacobis formel (28). Nödvändigheten av villkor (39) fastställs enligt följande. Av den positiva bestämheten hos formen följer den positiva bestämheten hos de "stympade" formerna

.

Men då måste alla dessa former vara icke-singular, d.v.s.

Nu har vi möjlighet att använda Jacobi-formeln (28) (för ). Eftersom på höger sida av denna formel måste alla kvadrater vara positiva, alltså

Detta innebär ojämlikheter (39). Teoremet har bevisats.

Eftersom valfri huvudmoll i en matris, med korrekt omnumrering av variabler, kan placeras i det övre vänstra hörnet, har vi

Följd. I positiv definitiv kvadratisk form är alla huvudminorer i koefficientmatrisen positiva:

Kommentar. Från icke-negativitet hos på varandra följande rektor minderåriga

följer inte formulärets icke-negativitet . Ja, formen

,

vart i , uppfyller villkoren , men är inte icke-negativ.

Det finns dock följande

Sats 4. För att en kvadratisk form ska vara icke-negativ, är det nödvändigt och tillräckligt att alla huvudsakliga biroller i dess koefficientmatris är icke-negativa:

Bevis. Låt oss införa en hjälpform som är icke-positiv, det är nödvändigt och tillräckligt att ojämlikheterna

Facebook

Twitter

I kontakt med

Klasskamrater

Google Plus