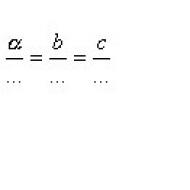svojstva primitivca. Antiderivativ i neodređeni integral, njihova svojstva
Rješavanje integrala je lak zadatak, ali samo za elitu. Ovaj je članak za one koji žele naučiti razumjeti integrale, ali znaju malo ili nimalo o njima. Integral... Zašto je potreban? Kako to izračunati? Što su određeni i neodređeni integrali? Ako je jedina upotreba integrala za koju znate da dobijete nešto korisno s teško dostupnih mjesta pomoću kuke u obliku integralne ikone, onda dobrodošli! Naučite kako riješiti integrale i zašto ne možete bez toga.
Proučavamo koncept "integralnog"
Integracija je bila poznata u starom Egiptu. Naravno, ne u modernom obliku, ali ipak. Od tada su matematičari napisali mnogo knjiga na tu temu. Osobito istaknuta Newton i Leibniza ali bit stvari se nije promijenila. Kako razumjeti integrale od nule? Nema šanse! Da biste razumjeli ovu temu, i dalje će vam trebati osnovno znanje o osnovama matematičke analize. Informacije o , koje su također potrebne za razumijevanje integrala, već su na našem blogu.
Neodređeni integral
Imajmo neku funkciju f(x) .
Neodređeni integral funkcije f(x) takva funkcija se zove F(x) , čija je derivacija jednaka funkciji f(x) .
Drugim riječima, integral je obrnuti derivat ili antiderivat. Usput, o tome kako čitati u našem članku.

Antiderivat postoji za sve kontinuirane funkcije. Također, antiderivatu se često dodaje predznak konstante, budući da se derivacije funkcija koje se razlikuju po konstanti poklapaju. Proces pronalaženja integrala naziva se integracija.
Jednostavan primjer:

Kako ne bi stalno izračunavali antiderivate elementarnih funkcija, prikladno ih je unijeti u tablicu i koristiti gotove vrijednosti.
Potpuna tablica integrala za studente

Određeni integral
Kada se bavimo konceptom integrala, imamo posla s beskonačno malim veličinama. Integral će vam pomoći izračunati površinu figure, masu nehomogenog tijela, put prijeđen tijekom neravnomjernog kretanja i još mnogo toga. Treba imati na umu da je integral zbroj beskonačno velikog broja beskonačno malih članova.
Kao primjer, zamislite graf neke funkcije. Kako pronaći površinu figure omeđenu grafom funkcije?

Uz pomoć integrala! Razbijmo krivolinijski trapez, omeđen koordinatnim osi i grafom funkcije, na beskonačno male segmente. Dakle, lik će biti podijeljen u tanke stupce. Zbroj površina stupova bit će površina trapeza. Ali zapamtite da će takav izračun dati približan rezultat. Međutim, što su segmenti manji i uži, to će izračun biti točniji. Ako ih smanjimo do te mjere da duljina teži nuli, tada će zbroj površina segmenata težiti površini figure. Ovo je definitivni integral koji se piše na sljedeći način:

Točke a i b nazivaju se granicama integracije.
 Bari Alibasov i grupa "Integral"
Bari Alibasov i grupa "Integral" Usput! Za naše čitatelje sada je popust od 10%.
Pravila za izračunavanje integrala za lutke
Svojstva neodređenog integrala
Kako riješiti neodređeni integral? Ovdje ćemo razmotriti svojstva neodređenog integrala, koja će biti korisna u rješavanju primjera.
- Derivat integrala jednak je integrandu:

- Konstanta se može izvaditi ispod predznaka integrala:

- Integral zbroja jednak je zbroju integrala. Također vrijedi za razliku:
Svojstva određenog integrala
- linearnost:

- Predznak integrala se mijenja ako se granice integracije obrnu:

- Na bilo koji bodova a, b i S:

Već smo saznali da je definitivni integral granica zbroja. Ali kako dobiti određenu vrijednost prilikom rješavanja primjera? Za to postoji Newton-Leibnizova formula:

Primjeri rješavanja integrala
U nastavku ćemo razmotriti nekoliko primjera pronalaženja neodređenih integrala. Nudimo da samostalno razumijemo zamršenost rješenja, a ako nešto nije jasno, postavljajte pitanja u komentarima.

Za konsolidaciju gradiva pogledajte video o tome kako se integrali rješavaju u praksi. Nemojte očajavati ako se integral ne da odmah. Obratite se profesionalnoj studentskoj službi i svaki trostruki ili krivocrtni integral na zatvorenoj površini bit će u vašoj moći.
Antiderivativna funkcija i neodređeni integral
Činjenica 1. Integracija je suprotna akcija diferencijaciji, odnosno obnavljanje funkcije iz poznate derivacije ove funkcije. Funkcija vraćena na ovaj način F(x) Zove se primitivni za funkciju f(x).
Definicija 1. Funkcija F(x f(x) na nekom intervalu x, ako za sve vrijednosti x iz ovog intervala jednakost F "(x)=f(x), odnosno ovu funkciju f(x) je derivacija antiderivativne funkcije F(x). .
Na primjer, funkcija F(x) = grijeh x je antiderivat za funkciju f(x) = cos x na cijeloj brojevnoj liniji, budući da za bilo koju vrijednost x (grijeh x)" = (cos x) .
Definicija 2. Neodređeni integral funkcije f(x) je skup svih njegovih antiderivata. Ovo koristi notaciju
∫
f(x)dx
,gdje je znak ∫ naziva se integralni znak, funkcija f(x) je integrand, i f(x)dx je integrand.
Dakle, ako F(x) je neki antideritiv za f(x), dakle
∫
f(x)dx = F(x) +C
gdje C - proizvoljna konstanta (konstanta).
Za razumijevanje značenja skupa antiderivata funkcije kao neodređenog integrala prikladna je sljedeća analogija. Neka budu vrata (tradicionalna drvena vrata). Njegova je funkcija "biti vrata". Od čega su vrata napravljena? Sa drveta. To znači da je skup antiderivata integranda "biti vrata", odnosno njegov neodređeni integral, funkcija "biti stablo + C", gdje je C konstanta, što u ovom kontekstu može označavati, za na primjer, vrsta drveća. Baš kao što su vrata napravljena od drveta s nekim alatima, derivacija funkcije je "napravljena" od antiderivativne funkcije s formulu koju smo naučili proučavajući izvedenicu .
Tada je tablica funkcija uobičajenih objekata i njihovih odgovarajućih primitiva ("biti vrata" - "biti drvo", "biti žlica" - "biti metal" itd.) slična tablici od osnovne neodređene integrale, koji će biti dati u nastavku. Tablica neodređenih integrala navodi uobičajene funkcije, naznačujući antiderivate od kojih su te funkcije "napravljene". U sklopu zadataka za pronalaženje neodređenog integrala dati su takvi integrandi koji se bez posebnih napora mogu integrirati izravno, odnosno prema tablici neodređenih integrala. U složenijim problemima integrand se najprije mora transformirati kako bi se mogli koristiti tablični integrali.
Činjenica 2. Vraćajući funkciju kao antiderivativ, moramo uzeti u obzir proizvoljnu konstantu (konstantu) C, a da ne biste napisali popis antiderivata s raznim konstantama od 1 do beskonačnosti, trebate zapisati skup antiderivata s proizvoljnom konstantom C, ovako: 5 x³+C. Dakle, proizvoljna konstanta (konstanta) je uključena u izraz antiderivata, budući da antiderivat može biti funkcija, na primjer, 5 x³+4 ili 5 x³+3 i kada se razlikuje 4 ili 3 ili bilo koja druga konstanta nestaje.
Postavili smo integracijski problem: za zadanu funkciju f(x) pronaći takvu funkciju F(x), čija izvedenica jednako je f(x).
Primjer 1 Pronađite skup antiderivata funkcije
Riješenje. Za ovu funkciju antiderivat je funkcija
Funkcija F(x) naziva se antiderivatom za funkciju f(x) ako je izvedenica F(x) jednako je f(x), ili, što je isto, diferencijal F(x) jednako je f(x) dx, tj.
![]() (2)
(2)
Stoga je funkcija antiderivativna za funkciju . Međutim, to nije jedini antideritiv za . Oni su također funkcije
gdje S je proizvoljna konstanta. To se može provjeriti diferencijacijom.
Dakle, ako postoji jedan antiderivat za funkciju, tada za nju postoji beskonačan skup antiderivata koji se razlikuju po konstantnom zbroju. Svi antiderivati za funkciju su napisani u gornjem obliku. To slijedi iz sljedećeg teorema.
Teorem (formalni iskaz činjenice 2). Ako F(x) je antiderivat za funkciju f(x) na nekom intervalu x, zatim bilo koji drugi antiderivat za f(x) na istom intervalu može se predstaviti kao F(x) + C, gdje S je proizvoljna konstanta.
U sljedećem primjeru već se okrećemo tablici integrala, koja će biti dana u paragrafu 3, nakon svojstava neodređenog integrala. To činimo prije nego što se upoznamo s cijelom tablicom, tako da je suština navedenog jasna. A nakon tablice i svojstava, koristit ćemo ih u cijelosti prilikom integracije.
Primjer 2 Pronađite skupove antiderivata:
Riješenje. Pronalazimo skupove antiderivativnih funkcija od kojih su te funkcije "napravljene". Kad se spominju formule iz tablice integrala, za sada samo prihvatite da takve formule postoje, a mi ćemo malo dalje proučiti tablicu neodređenih integrala u cijelosti.
1) Primjenom formule (7) iz tablice integrala za n= 3, dobivamo
![]()
2) Koristeći formulu (10) iz tablice integrala za n= 1/3, imamo
3) Budući da
onda prema formuli (7) at n= -1/4 nađi
![]()
Pod znakom integrala ne pišu samu funkciju f, a njegov proizvod diferencijalom dx. To se prvenstveno radi kako bi se naznačilo koja se varijabla traži za antiderivatom. Na primjer,
![]() ,
,
![]() ;
;
ovdje je u oba slučaja integrand jednak , ali njegovi neodređeni integrali u razmatranim slučajevima ispadaju različiti. U prvom slučaju, ova funkcija se smatra funkcijom varijable x, au drugom - u funkciji z .
Proces nalaženja neodređenog integrala funkcije naziva se integriranjem te funkcije.
Geometrijsko značenje neodređenog integrala
Neka je potrebno pronaći krivulju y=F(x) a već znamo da je tangenta nagiba tangente u svakoj njezinoj točki zadana funkcija f(x) apscisa ove točke.
Prema geometrijskom značenju derivacije, tangenta nagiba tangente u danoj točki na krivulji y=F(x) jednaka vrijednosti izvedenice F"(x). Dakle, moramo pronaći takvu funkciju F(x), za koji F"(x)=f(x). Potrebna funkcija u zadatku F(x) je izvedeno iz f(x). Uvjet problema ne zadovoljava jedna krivulja, već obitelj krivulja. y=F(x)- jedna od ovih krivulja, kao i svaka druga krivulja može se dobiti iz nje paralelnim prevođenjem duž osi Oy.
Nazovimo graf antiderivativne funkcije od f(x) integralna krivulja. Ako F"(x)=f(x), zatim graf funkcije y=F(x) je integralna krivulja.
Činjenica 3. Neodređeni integral geometrijski je predstavljen obitelji svih integralnih krivulja kao na slici ispod. Udaljenost svake krivulje od ishodišta određena je proizvoljnom konstantom (konstantom) integracije C.

Svojstva neodređenog integrala
Činjenica 4. Teorem 1. Derivat neodređenog integrala jednak je integrandu, a njegov diferencijal jednak je integrandu.
Činjenica 5. Teorem 2. Neodređeni integral diferencijala funkcije f(x) jednaka je funkciji f(x) do konstantnog člana , tj.
![]() (3)
(3)
Teoremi 1 i 2 pokazuju da su diferencijacija i integracija međusobno inverzne operacije.
Činjenica 6. Teorem 3. Konstantni faktor u integrandu može se izvaditi iz predznaka neodređenog integrala , tj.
Za svaku matematičku radnju postoji inverzna radnja. Za djelovanje diferencijacije (nalaženje derivacija funkcija) postoji i inverzno djelovanje – integracija. Integracijom se funkcija pronalazi (obnavlja) pomoću njezine zadane derivacije ili diferencijala. Pronađena funkcija se poziva primitivni.
Definicija. Diferencibilna funkcija F(x) naziva se antiderivatom za funkciju f(x) na zadanom intervalu, ako za sve x iz ovog intervala vrijedi jednakost: F′(x)=f (x).
Primjeri. Nađi antiderivate za funkcije: 1) f (x)=2x; 2) f(x)=3cos3x.
1) Budući da (x²)′=2x, onda će, po definiciji, funkcija F (x)=x² biti antiderivat za funkciju f (x)=2x.
2) (sin3x)′=3cos3x. Ako označimo f (x)=3cos3x i F (x)=sin3x, tada, prema definiciji antiderivacije, imamo: F′(x)=f (x), pa je, prema tome, F (x)=sin3x antiderivat za f ( x)=3cos3x.
Imajte na umu da i (sin3x +5 )′= 3cos3x, i (sin3x -8,2 )′= 3cos3x, ... u općem obliku možemo napisati: (sin3x +C)′= 3cos3x, gdje S je neka konstantna vrijednost. Ovi primjeri govore o dvosmislenosti djelovanja integracije, za razliku od djelovanja diferencijacije, kada bilo koja diferencijabilna funkcija ima jednu derivaciju.
Definicija. Ako je funkcija F(x) je antiderivat za funkciju f(x) na nekom intervalu, tada skup svih antiderivata ove funkcije ima oblik:
F(x)+C gdje je C bilo koji realan broj.
Skup svih antiderivata F (x) + C funkcije f (x) na intervalu koji se razmatra naziva se neodređenim integralom i označava se simbolom ∫ (integralni znak). Zapiši: ∫f (x) dx=F (x)+C.
Izraz ∫f(x)dx glasi: "integral ef od x do de x".
f(x)dx je integrand,
f(x) je integrand,
x je varijabla integracije.
F(x) je antiderivat za funkciju f(x),
S je neka konstantna vrijednost.
Sada se razmatrani primjeri mogu napisati na sljedeći način:
1) ∫ 2hdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.
Što znači znak d?
d- diferencijalni znak - ima dvostruku svrhu: prvo, ovaj znak odvaja integrand od integracijske varijable; drugo, sve iza ovog znaka se zadano razlikuje i množi s integrandom.
Primjeri. Nađi integrale: 3) ∫ 2pxdx; 4) ∫ 2pxdp.
3) Nakon ikone diferencijala d troškovi xx, a R
∫ 2hrdx=px²+S. Usporedite s primjerom 1).
Napravimo provjeru. F′(x)=(px²+C)′=p (x²)′+C′=p 2x=2px=f (x).
4) Nakon ikone diferencijala d troškovi R. Dakle, varijabla integracije R, i množitelj x treba smatrati konstantnom vrijednošću.
∫ 2hrdr=r²h+S. Usporedite s primjerima 1) i 3).
Napravimo provjeru. F′(p)=(p²x+C)′=x (p²)′+C′=x 2p=2px=f (p).
Vidjeli smo da derivacija ima brojne primjene: derivacija je brzina kretanja (ili, općenito, brzina bilo kojeg procesa); derivacija je nagib tangente na graf funkcije; pomoću izvedenice možete istražiti funkciju za monotonost i ekstreme; Izvod pomaže u rješavanju problema optimizacije.
Ali u stvarnom životu treba rješavati i inverzne probleme: na primjer, uz problem pronalaženja brzine iz poznatog zakona gibanja, postoji i problem vraćanja zakona gibanja iz poznate brzine. Razmotrimo jedan od ovih problema.
Primjer 1 Materijalna točka kreće se ravnom linijom, a brzina njezina kretanja u trenutku t dana je formulom u = tg. Pronađite zakon gibanja.
Riješenje. Neka je s = s(t) željeni zakon gibanja. Poznato je da je s"(t) = u"(t). Dakle, da bismo riješili problem, moramo izabrati funkcija s = s(t), čija je derivacija jednaka tg. Lako je to pogoditi
Odmah napominjemo da je primjer riješen točno, ali nepotpuno. Dobili smo da U stvari, problem ima beskonačno mnogo rješenja: bilo koju funkciju oblika ![]() proizvoljna konstanta, može poslužiti kao zakon gibanja, jer
proizvoljna konstanta, može poslužiti kao zakon gibanja, jer

Da bismo zadatak učinili konkretnijim, morali smo popraviti početnu situaciju: naznačiti koordinatu pokretne točke u nekom trenutku vremena, na primjer, u t=0. Ako je, recimo, s (0) = s 0, tada iz jednakosti dobivamo s (0) = 0 + C, tj. S 0 \u003d C. Sada je zakon gibanja jednoznačno definiran:
U matematici se međusobno obrnutim operacijama daju različita imena, izmišljaju se posebne oznake: na primjer, kvadriranje (x 2) i izvlačenje kvadratnog korijena sinusa (sinx) i arcsinus(arcsin x) itd. Proces nalaženja derivacije s obzirom na zadanu funkciju naziva se diferencijacija, a inverzna operacija, t.j. proces nalaženja funkcije zadanom derivacijom – integracijom.
Sam izraz "derivacija" može se opravdati "na svjetovni način": funkcija y - f (x) "proizvodi" novu funkciju y "= f" (x) Funkcija y \u003d f (x) djeluje kao da kao "roditelj" , ali matematičari ga, naravno, ne zovu "roditelj" ili "proizvođač", oni kažu da je u odnosu na funkciju y "=f" (x), primarna slika, ili , ukratko, antiderivativ.
Definicija 1. Funkcija y = F (x) naziva se antiderivatom za funkciju y = f (x) na danom intervalu X, ako je za sve x iz X istinita jednakost F "(x) \u003d f (x) .
U praksi, interval X obično nije specificiran, već se podrazumijeva (kao prirodna domena funkcije).
Evo nekoliko primjera:
1) Funkcija y = x 2 je antiderivat za funkciju y = 2x, budući da je za sve x istinita jednakost (x 2) "\u003d 2x.
2) funkcija y - x 3 je antiderivat za funkciju y-3x 2, budući da je za sve x jednakost (x 3)" \u003d 3x 2 istinita.
3) Funkcija y-sinx je antiderivat za funkciju y=cosx, budući da za sve x vrijedi jednakost (sinx) "=cosx.
4) Funkcija je antiderivativna za funkciju na intervalu jer je za sve x > 0 jednakost istinita
Općenito, poznavajući formule za pronalaženje derivata, nije teško sastaviti tablicu formula za pronalaženje antiderivata.

Nadamo se da razumijete kako je ova tablica sastavljena: derivacija funkcije koja je napisana u drugom stupcu jednaka je funkciji koja je napisana u odgovarajućem retku prvog stupca (provjerite, ne budi lijen, to je jako korisno). Na primjer, za funkciju y \u003d x 5, antiderivat je, kako ste ustanovili, funkcija (vidi četvrti red tablice).
Bilješke: 1. U nastavku dokazujemo teorem da ako je y = F(x) antiderivat za funkciju y = f(x), onda funkcija y = f(x) ima beskonačno mnogo antiderivata i svi imaju oblik y = F (x ) + C. Stoga bi bilo ispravnije dodati pojam C posvuda u drugom stupcu tablice, gdje je C proizvoljan realni broj.
2. Radi kratkoće, ponekad umjesto izraza "funkcija y = F(x) je antiderivat za funkciju y = f(x)", kažu da je F(x) antiderivat za f(x) ".
2. Pravila za pronalaženje antiderivata
Pri traženju antiderivata, kao i pri traženju izvedenica, ne koriste se samo formule (navedene su u tablici na str. 196), već i neka pravila. Oni su izravno povezani s odgovarajućim pravilima za računanje izvedenica.
Znamo da je derivacija zbroja jednaka zbroju derivacija. Ovo pravilo generira odgovarajuće pravilo za pronalaženje antiderivata.
Pravilo 1 Antiderivat zbroja jednak je zbroju antiderivata.
Skrećemo vam pozornost na neku "lakoću" ove formulacije. Zapravo, bilo bi potrebno formulirati teorem: ako funkcije y = f(x) i y=g(x) imaju antiderivacije na intervalu X, odnosno yF(x) i yG(x), tada je zbroj funkcija y = f(x) + g(x) ima antiderivat na intervalu X, a taj antiderivat je funkcija y = F(x) + G(x). Ali obično se pri formuliranju pravila (a ne teorema) ostavljaju samo ključne riječi - to je prikladnije za primjenu pravila u praksi.
Primjer 2 Nađi antiderivat za funkciju y = 2x + cos x.
Riješenje. Antiderivat za 2x je x "; antiderivat za cosx je sin x. Dakle, antiderivat za funkciju y = 2x + cos x bit će funkcija y = x 2 + sin x (i općenito bilo koja funkcija od oblik Y \u003d x 1 + sinx + C) .
Znamo da se konstantni faktor može izvaditi iz predznaka derivacije. Ovo pravilo generira odgovarajuće pravilo za pronalaženje antiderivata.
Pravilo 2 Konstantni faktor se može izvaditi iz predznaka antiderivacije.
Primjer 3
Riješenje. a) Antiderivat za sin x je -cos x; dakle, za funkciju y \u003d 5 sin x, antiderivat će biti funkcija y = -5 cos x.
b) Antiderivat za cos x je sin x; dakle, za antiderivativnu funkciju bit će funkcija
c) Antiderivat za x 3 je antiderivat za x je antiderivat za funkciju y \u003d 1 je funkcija y \u003d x. Koristeći prvo i drugo pravilo za pronalaženje antiderivata, dobivamo da je antiderivat za funkciju y \u003d 12x 3 + 8x-1 funkcija
Komentar. Kao što znate, derivacija proizvoda nije jednaka umnošku izvedenica (pravilo za razlikovanje proizvoda je kompliciranije) i derivacija kvocijenta nije jednaka kvocijentu izvedenica. Stoga ne postoje pravila za pronalaženje antiderivata proizvoda ili antiderivata kvocijenta dviju funkcija. Budi oprezan!
Dobivamo još jedno pravilo za pronalaženje antiderivata. Znamo da se derivacija funkcije y \u003d f (kx + m) izračunava po formuli
Ovo pravilo generira odgovarajuće pravilo za pronalaženje antiderivata.
Pravilo 3 Ako je y = F (x) antiderivat za funkciju y = f (x), tada je antiderivat za funkciju y = f (kx + m) funkcija
Doista,
![]()
To znači da je antiderivat za funkciju y = f (kx + m).
Značenje trećeg pravila je sljedeće. Ako znate da je antiderivat za funkciju y = f (x) funkcija y = F (x), a trebate pronaći antiderivat funkcije y = f (kx + m), nastavite kao slijedi: uzeti istu funkciju F, ali umjesto argumenta x zamijeniti izraz xx+m; osim toga, nemojte zaboraviti napisati "korekcioni faktor" prije predznaka funkcije
Primjer 4 Pronađite antiderivate za zadane funkcije:
Riješenje, a) Antiderivat za sin x je -cos x; to znači da će za funkciju y \u003d sin2x antiderivat biti funkcija
b) Antiderivat za cos x je sin x; dakle, za antiderivativnu funkciju bit će funkcija
![]()
c) Antiderivat za x 7 je dakle, za funkciju y = (4-5x) 7, antiderivat će biti funkcija
3. Neodređeni integral
Gore smo već napomenuli da problem nalaženja antiderivata za danu funkciju y = f(x) ima više od jednog rješenja. Razmotrimo ovo pitanje detaljnije.
Dokaz. 1. Neka je y \u003d F (x) antiderivat za funkciju y \u003d f (x) na intervalu X. To znači da je za sve x iz X jednakost x "(x) = f (x) istina. Pronađite derivaciju bilo koje funkcije oblika y = F (x) + C:
(F (x) + C) \u003d F "(x) + C \u003d f (x) + 0 \u003d f (x).
Dakle, (F(x)+C) = f(x). To znači da je y \u003d F (x) + C antiderivat za funkciju y \u003d f (x).
Dakle, dokazali smo da ako funkcija y = f (x) ima antiderivat y = F (x), tada funkcija (f = f (x) ima beskonačno mnogo antiderivata, na primjer, bilo koja funkcija oblik y \u003d F (x) +C je antiderivat.
2. Dokažimo sada da se cijeli skup antiderivata iscrpljuje navedenim tipom funkcija.
Neka su y=F 1 (x) i y=F(x) dva antiderivata za funkciju Y = f(x) na intervalu X. To znači da za sve x iz intervala X vrijede sljedeće relacije: F^( x) = f (X); F "(x) \u003d f (x).
Uzmimo u obzir funkciju y = F 1 (x) -.F (x) i pronađimo njezinu derivaciju: (F, (x) -F (x)) "\u003d F [(x) - F (x) \u003d f (x) - f(x) = 0.
Poznato je da ako je derivacija funkcije na intervalu X identično jednaka nuli, tada je funkcija konstantna na intervalu X (vidi Teorem 3 u § 35). Dakle, F 1 (x) -F (x) \u003d C, tj. Fx) \u003d F (x) + C.
Teorem je dokazan.
Primjer 5 Postavljen je zakon promjene brzine od vremena v = -5sin2t. Nađite zakon gibanja s = s(t) ako je poznato da je u trenutku t=0 koordinata točke bila jednaka broju 1,5 (tj. s(t) = 1,5).
Riješenje. Budući da je brzina derivacija koordinate u funkciji vremena, prvo trebamo pronaći antiderivat brzine, t.j. antiderivat za funkciju v = -5sin2t. Jedan od takvih antiderivata je funkcija , a skup svih antiderivata ima oblik:
Da bismo pronašli određenu vrijednost konstante C, koristimo se početnim uvjetima prema kojima je s(0) = 1,5. Zamjenom u formuli (1) vrijednosti t=0, S = 1,5, dobivamo:
Zamjenom pronađene vrijednosti C u formulu (1) dobivamo zakon gibanja koji nas zanima:
Definicija 2. Ako funkcija y = f(x) ima antiderivat y = F(x) na intervalu X, tada je skup svih antiderivata, t.j. skup funkcija oblika y \u003d F (x) + C, naziva se neodređenim integralom funkcije y \u003d f (x) i označava se:
(čitaju: “neodređeni integral ef od x de x”).
U sljedećem odjeljku saznat ćemo koje je skriveno značenje ove oznake.
Na temelju tablice antiderivata koja je dostupna u ovom odlomku, sastavit ćemo tablicu osnovnih neodređenih integrala:

Na temelju gornja tri pravila za pronalaženje antiderivata možemo formulirati odgovarajuća pravila integracije.
Pravilo 1 Integral zbroja funkcija jednak je zbroju integrala ovih funkcija:
Pravilo 2 Konstantni faktor se može izvaditi iz predznaka integrala:
![]()
Pravilo 3 Ako

Primjer 6 Nađi neodređene integrale:
Riješenje, a) Koristeći prvo i drugo integracijsko pravilo, dobivamo:
![]()
Sada koristimo 3. i 4. integracijsku formulu:
![]()
Kao rezultat, dobivamo:
![]()
b) Koristeći treće pravilo integracije i formulu 8, dobivamo:

c) Za izravno određivanje zadanog integrala nemamo ni odgovarajuću formulu ni odgovarajuće pravilo. U takvim slučajevima ponekad pomažu preliminarne identične transformacije izraza sadržanog pod znakom integrala.
Koristimo trigonometrijsku formulu za smanjenje stupnja:
Zatim uzastopno nalazimo:

A.G. Mordkovich algebra 10. razred
Kalendarsko-tematsko planiranje u matematici, video u matematici online , Matematika u školi
Definicija 1. Funkcija F(x) Zove se antiderivat za funkciju f(x) na nekom intervalu ako je u svakoj točki ovog intervala funkcija F(x) je diferencijabilna i jednakost F "(x) = f(x).
Primjer 1 Funkcija F(x) = grijeh x je antiderivat funkcije f(x) = cos x na beskonačnom intervalu (- ¥; +¥), budući da
F’(x) = (grijeh x)" = cos x = f(x) za x Î (– ¥;+¥).
Lako je provjeriti da su funkcije F 1 (x) = grijeh x+ 5 i F 2 (x) = grijeh x– 10 su također antiderivati funkcije f(x) = cos x za sve (– ¥; + ¥), tj. ako za funkciju f(x) postoji antiderivat funkcije na nekom intervalu, onda nije jedinstven. Dokažimo da je skup svih antiderivata za zadanu funkciju f(x) je skup koji je zadan formulom F(x) + C, gdje C je bilo koja konstantna vrijednost.
Teorem 1 (o općem obliku antiderivata). Neka F(x) je jedan od antiderivata za funkciju f(x) na intervalu ( a;b). Zatim bilo koji drugi antiderivat za funkciju f(x) na intervalu ( a;b) prikazan je u obliku F(x) + C, gdje C- neki broj.
Dokaz. Prvo, provjerimo to F(x) + C je također antiderivativ za funkciju f(x) na intervalu ( a;b).
Prema teoremu F(x) na intervalu ( a;b f(x), pa vrijedi sljedeća jednakost:
F "(x) = f(x) za bilo koji xÎ ( a;b).
Jer S je onda neki broj
(F(x) + S) " = F"(x)+S" = F "(x) + 0 = f(x).
Iz čega slijedi: ( F(x) + C)" = f(x) za bilo koji xÎ ( a;b), što znači F(x) + S na intervalu ( a;b) je antiderivativ za funkciju f(x).
Drugo, provjeravamo da li F(x) i F( x) su dva antiderivata za funkciju f(x) na intervalu ( a;b), tada se međusobno razlikuju po konstantnoj vrijednosti, t.j. F(x) – F( x) = konst.
Označimo j( x) = F(x) – F( x). Budući da je po pretpostavci funkcije F(x) i F( x) antiderivati na intervalu ( a;b) za funkciju f(x), tada vrijede sljedeće jednakosti: F "(x) = f(x) i F"( x) = f(x) za bilo koji xÎ ( a;b). Stoga j"( x) = F "(x) – F" ( x) = f(x) – f(x) = 0 za bilo koji xÎ ( a;b).
Funkcija j( x) je kontinuiran i diferenciran za xÎ ( a;b). Dakle, na bilo kojem segmentu [ x 1 ; x 2 ] M ( a; b) funkcija j( x) zadovoljava Lagrangeov teorem: postoji točka n( x 1 ; x 2), za koje vrijedi jednakost:
j( x 2) – j( x 1) = j" () × ( x 2 – x 1) = 0×( x 2 – x 1) = 0
Þ j( x 2) – j( x 1) = 0 z j( x 2) = j( x 1) Þ j( x) = konst.
Sredstva, F(x) – F( x) = konst.
Dakle, dobili smo to ako je poznat jedan antiderivat F(x) za funkciju f(x) na intervalu ( a;b), tada se bilo koji drugi antiderivat može predstaviti kao F(x) + S, gdje S je proizvoljna konstantna vrijednost. Ovaj oblik pisanja primitivne tzv opći tip primitivca.
Pojam neodređenog integrala
Definicija 2. Skup svih antiderivata za zadanu funkciju f(x) na intervalu ( a;b) Zove se neodređeni integral funkcije f(x) na ovom intervalu i označen je simbolom:
![]()
U oznaci se znak zove integralni znak, – integrand, – integrand, – integracijska varijabla.
Teorem 2. Ako je funkcija f(x) kontinuirano je na intervalu ( a;b), tada ima na intervalu ( a;b) antiderivativ i neodređeni integral.
Komentar. Operacija pronalaženja neodređenog integrala zadane funkcije f(x) na nekom intervalu naziva se integracija funkcije f(x).
Svojstva neodređenog integrala
Iz definicija antiderivata F(x) i neodređeni integral ove funkcije f(x) na nekom intervalu slijede svojstva neodređenog integrala:
1. ![]() .
.
2. ![]() .
.
3. ![]() , gdje S je proizvoljna konstanta.
, gdje S je proizvoljna konstanta.
4. ![]() , gdje k= konst.
, gdje k= konst.
Komentar. Sva gornja svojstva su točna pod uvjetom da se integrali koji se pojavljuju u njima razmatraju na istom intervalu i postoje.
Tablica osnovnih neodređenih integrala
Djelovanje integracije suprotno je djelovanju diferencijacije, t.j. s obzirom na zadanu derivaciju funkcije f(x) potrebno je vratiti početnu funkciju F(x). Tada iz definicije 2 i tablice derivacija (vidi §4, točka 3, str. 24) dobivamo tablica osnovnih integrala.
3.  .
.
4. ![]() .
.